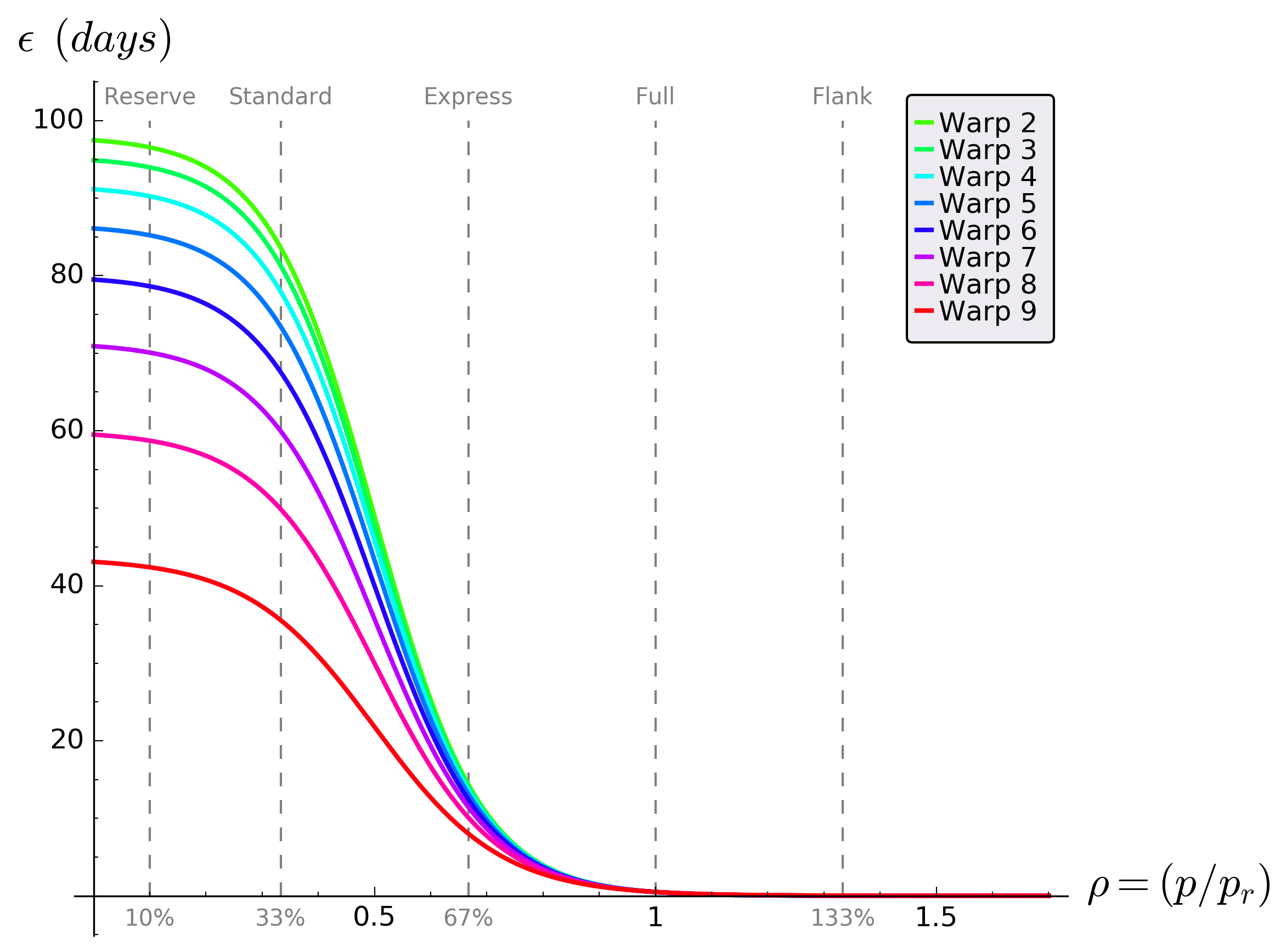
Introduction
The need to convey letters of an alphabet verbally is a common occurrence. You are on the phone and need to spell a name, car registration number or email address. If you are an English speaker, you will probably be struggling with phases like “‘d’ for ‘dog'” or “‘f’ for ‘Fred'”.
You may just choose to sound the letters directly as ‘de’, ‘ef’, etc. and hope they will be received correctly. With today’s modern, and generally high quality, voice networks this strategy is often successful but occasionally there are misheard letters and you are back to finding a word that represents them or repeating them more slowing and distinctly.
The problem occurs in all languages but this blog will focus on English. However, the principles should be easily transferred to other languages.
How to reliably transmit data over a noisy channel is a well known and much studied problem. The general approach is to include additional information with the original data. This additional or redundant information is used to recover the original data should it be affected during transmission. The trade-off is this additional information makes the transmission longer. So the challenge is to formulate this additional information in a ways that keep the transmission as short as possible but provides the best chance to recover the data should it become corrupted. In the digital domain this comes under the study of Coding Theory.
For our purposes, the additional data is in the form of a word which is used to represent a letter. A word is longer and has more sounds which makes it much easier to identify and less likely to be confused over a noisy background. The words chosen need to be:
- Known by the speaker and recipient
- Clearly associated with a letter either by agreement or implication
- Sufficiently distinct from each another to improve differentiation and recognition
- No longer than necessary for expediency
The first for these is accommodated by using well known common words, the second by treating the first letter of the word as the representative letter and the last two are the main design challenge.
Obviously using say, “pat” for “p” and “bat” for “b” is not particularly effective as “pat” and “bat” might themselves be confused. Whereas, for example, “pen” and “bat” seem to be more distinct.
Using long words would make the distinction even greater, for example, “banana” and “pendulum”, however these take longer to say and hence slow down the transmission process. So there is a trade-off between speed and accuracy.
We can summarise the goals of an effective International Spelling Alphabet (or word replacement scheme for letters) as:
- Use common words easily recognised by both parties
- Use short words to speed communications
- Use words that are phonetically distinct to minimise confusion
Some Existing Examples
International Spelling Alphabet
International Spelling Alphabet (ISA), also known as the NATO Phonetic Alphabet, is widely used in aviation, military and other areas where accurate letter transmission is critical. Most people are familiar with it, even if they don’t remember all the words. It was developed in the 1950’s and hasn’t changed since.
a - alfa n - november
b - bravo o - oscar
c - charlie p - papa
d - delta q - quebec
e - echo r - romeo
f - foxtrot s - sierra
g - golf t - tango
h - hotel u - uniform
i - india v - victor
j - juliett w - whiskey
k - kilo x - x-ray
l - lima y - yankee
m - mike z - zulu
Note the deliberate misspelling of alfa (alpha) and juliett (juliet/juliette) to help clarify pronunciation for non-native English speakers.
Hexadecimal
When I started in IT, many years ago, I was taught to use the following words to represent the six hexadecimal letters:
a - able
b - baker
c - charlie
d - dog
e - easy
f - fox
We used these to read out hexadecimal character strings, which are conventionally represented by the sixteen characters 0-9, A-F. This worked well as they are quite short, easy to say and fairly distinct.
Later I discovered they came from the earlier US Phonetic Alphabet (USPA) which was replaced by the ISA (above) in 1956. As can be seen from the reference, there were several variations and names of these early alphabets. In this article we will use USPA to refer to the following words:
a - able n - nan
b - baker o - oboe
c - charlie p - peter
d - dog q - queen
e - easy r - roger
f - fox s - sugar
g - george t - tare
h - how u - uncle
i - item v - victor
j - jig w - william
k - king x - x-ray
l - love y - yoke
m - mike z - zebra
Alternative Approach
Some reasons to consider an alternative to the ISA, especially for more casual use, include:
- Replacing the somewhat dated words and names with more contemporary and ‘politically correct’ alternatives
- Using shorter words with fewer syllables to improve communication speed (especially given the higher quality of modern voice channels)
- Selecting words with a verifiable minimum phonetic distance to optimise clarity
The approach used here is basically as follows:
- Select a list of candidate words (at least one for each letter)
- Convert them to a phonetic representation
- Select one word for each letter from the candidate words that minimises word length and maximises phonetic distance
As will be seen each of these steps involve some unique challenges. Just selecting a pool of suitable words for the first step is more involved than you might expect.
The second step requires a dictionary with phonetic representation of the words. As mentioned, this blog is primarily focussed on English. But as any English speaker knows there are many dialects of English each with their particular pronunciation. So the phonetic dictionary used will influence the outcome, but in most cases this shouldn’t be a major issue. Of course the same approach could be used for any language which has a suitable phonetic dictionary.
The last step has three separate problems:
- How to define the phonetic distance between two words
- How to define a effective ‘cost/benefit’, or quality, function that captures the trade-off between word length and phonetic distance
- How to select words to maximise this function
Disclaimer
Linguistics and its sub-field, phonology, are very mature subjects that have been extensively research and studied. The whole area has been re-examined and revised by the development of speech recognition technology that has introduce powerful mathematical tools and computing techniques that have further enhanced the field. So what follows should be seen, at best, as a simplification and generalisation of a much deeper and more complex discipline. Having said that, the use of convolution, a signal processing technique, to determine the phonetic distance between words (which accommodates phoneme duration) could be of some interest to the reader.
Finally, please note I’m not a professional linguist so don’t take the following as definitive.
Phonetic Dictionary
Carnegie Mellon University (CMU) has developed a large open source Pronouncing Dictionary. It has over 130,000 words presented in a format that is easy to process. It uses the ARPAbet phonetics set, which is based on US English, rather than the more general International Phonetic Alphabet but there are conversion tables between the two systems.
This post will use the CMU dictionary as its phonetic base. It is biased to US English pronunciation (not ideal for the Queen’s English purists:) but as we are only considering relative phonetic distances it shouldn’t be a significant issue.
Below is a small extract from the dictionary to show its structure:
...
DOG D AO1 G
DOGS D AO1 G Z
DOGAN D OW1 G AH0 N
DOGBANE D AO1 G B EY2 N
DOGBERRY D AO1 G B EH2 R IY0
DOGE D OW1 JH
DOGEAR D AA1 G IY0 R
DOGEARED D AA1 G IY0 R D
DOGEARING D AA1 G IY0 R IH0 NG
DOGEARS D AA1 G IY0 R Z
DOGFIGHT D AA1 G F AY2 T
DOGFIGHTS D AO1 G F AY2 T S
DOGFISH D AO1 G F IH2 SH
DOGGED D AO1 G D
DOGGEDLY D AO1 G AH0 D L IY0
...
The English language uses around 40 separate sounds or phonemes. They are divided into two main categories – consonants and vowels.
The CMU dictionary represents consonants as one or two character codes (starting with a consonants). Vowels are represented by three character codes (starting with a vowel) with the last character being a number indicating the degree of stress:
0 - No stress
1 - Primary stress
2 - Secondary stress
Each word is on a separate line and comment lines begin with a semicolon (;).
To get a feel for the number and distribution of phonemes, Table 1 below shows phoneme counts and percentages, split by phoneme type–consonant (con) or vowel (vow)–and ordered by frequency (high to low) for the entire CMU dictionary. Note the vowel stress number has been ignored, that is, the vowel counts are the sum of the three different stress values for each vowel.
|
|
Table 1 CMU phoneme frequency
We can see there are 39 phonemes in total – 24 consonants and 15 vowels. The most commonly used consonant is N as in “night” and the most common vowel is AH as in “duck”.
The full table of CMU phonemes and examples of their use is shown in Table 2 below.
|
|
Table 2 CMU phoneme description
Phonetic Distance between Words
Let’s consider two words w1 and w2 which have an associated list of phonemes (as determine for the phonetic dictionary) of length m and n respectively:
w1 = p1, p2, ..., pm
w2 = q1, q2, ..., qn
There are various ways to define a distance between two sequences of elements (phonemes here). One of the best known is Levenshtein distance which counts the number of changes required convert one sequence to the other. However, in this case we would like a more nuanced approach that is capable of incorporating the following characteristics:
- differences between individual phonemes (i.e. some phonemes are more likely to be confused than others)
- consideration of the order the phonemes occur within the sequence
- ability to accommodate some notion of phoneme duration
This suggests treating the phoneme sequence as more of a signal. This coincides with the brain processes the sound of a word. Convolution is a common technique in signal processing and can be adapted here to provide an alternative way to define the distance between the two sequences. The basic idea is to ‘slide’ the two sequences over one another and to calculate a distance value based on the sum of the ‘distance’ between orthogonal pairs of phonemes. The minimum value become the distance for the sequences.
Consider an example of the two sequences (p1, p2, p3) and (q1, q2). These produce the four match-ups as the sequences slide across:
-- p1 p2 p3 | p1 p2 p3 | p1 p2 p3 | p1 p2 p3 --
q1 q2 -- -- | q1 q2 -- | -- q1 q2 | -- -- q1 q2
The distances for each of the four would be, in order:
| 1. d(–,q1) + d(p1,q2) + d(p2,–) + d(p3,–) |
| 2. d(p1,q1) + d(p2,q2) + d(p3,–) |
| 3. d(p1,–) + d(p2,q1) + d(p3,q2) |
| 4. d(p1,–) + d(p2,–) + d(p3,q1) + d(–,q2) |
where d(x,y) = distance between two individual phonemes and ‘–’ represents a null (or missing) phoneme.
The example above considers each phoneme as a single discrete unit with the same fixed length. More realistically, phonemes are of varying duration. The convolution approach can be extended to accommodate this by repeating the phonemes a number of times based on their duration. This is akin to sampling the word more frequently in a signal processing sense. Using the example above, with durations p1=3, p2=5, p3=4, q1=5 and q2=3, two consecutive example matches would be:
... | p1 p1 p1 p2 p2 p2 p2 p2 p3 p3 p3 p3 | p1 p1 p1 p2 p2 p2 p2 p2 p3 p3 p3 p3 | ...
... | -- q1 q1 q1 q1 q1 q2 q2 q2 -- -- -- | -- -- q1 q1 q1 q1 q1 q2 q2 q2 -- -- | ...
For brevity, the remaining convolution matches are not shown.
The next step is to define the distance between individual phonemes. There are three main types:
- Consonants
- Vowels
- Null (‘–’ in the above examples)
Let’s assume all distances will fall in the range 0 to 1. That is:
| 0 ≤ d(x,y) ≤ 1 for all x, y ∈ Phonemes |
As consonants and vowels are considered quite separate in the literature, we will make their distance the maximum 1.0. More precisely:
| d(c,v) = d(v,c) = 1 for all c ∈ Consonants and v ∈ Vowels |
For null matches, the main consideration is that it should be set high enough to make a complete mismatch greater than a partial match so that there is always a minimum distance. Using the example above we want no overlap:
-- -- p1 p2 p3
q1 q2 -- -- --
to be a greater distance than at least one matching cases such as full overlap:
p1 p2 p3
q1 q2 --
If we generalise this to two phoneme sequences of length m and n with m ≥ n (without loss of generality) and let k = d(–,x) = d(x,–) we have (left hand side is no overlap and the right side is full overlap):
| k(m+n) ≥ k(m-n) + nd(x,y) | |
| km + kn ≥ km – kn + nd(x,y) | |
| kn ≥ -kn + nd(x,y) | |
| 2kn ≥ nd(x,y) | |
| 2k ≥ d(x,y) | (as n > 0) |
| k ≥ d(x,y)/2 | |
| k ≥ 0.5 | (as max(d(x,y)) = 1.0) |
So we need k greater than or equal to 0.5 and less than 1.0. We can take the middle ground and define k = d(–,x) = d(x,–) = 0.75. Table 3 below summarises the distances for combinations of phoneme pairs where c1 and c2 are consonants, and v1 and v2 are vowels.
| Phoneme | c2 | v2 | null (–) |
|---|---|---|---|
| c1 | dc(c1,c2) | 1.00 | 0.75 |
| v1 | 1.00 | dv(v1,v2) | 0.75 |
| null (–) | 0.75 | 0.75 | 0.00 |
Table 3 Phoneme pair distances
For completeness, the distance between two nulls, d(–,–), is defined as zero, however, as this situation never arises in this analysis it is irrelevant.
Distance function
In mathematics, the distance function is a mapping of pairs for elements (x,y) to a real number with the following conditions:
| 1. d(x,y) ≥ 0 | |
| 2. d(x,y) = 0 if and only if x = y | |
| 3. d(x,y) = d(y,x) | (symmetric) |
| 4. d(a,b) + d(b,c) ≥ d(a,c) | (triangle inequality) |
It is clear from the distance table above that conditions 1, 2 and 3 apply provided dc and dv comply with these distance metrics. With this assumption condition 4 (triangle inequality) also holds as can be seen for the following table that enumerates all 27 combinations of a, b and c:
| a | b | c | d(a,b) + d(b,c) ≥ d(a,c) | Substitute | Simpified | Triangle Inequality |
|---|---|---|---|---|---|---|
| c | c | c | d(c,c) + d(c,c) ≥ d(c,c) | dc(c1,c2) + dc(c2,c3) ≥ dc(c1,c3) | dc(c1,c2) + dc(c2,c3) ≥ dc(c1,c3) | ✓ |
| c | c | v | d(c,c) + d(c,v) ≥ d(c,v) | dc(c1,c2) + 1.0 ≥ 1.0 | dc(c1,c2) ≥ 0.0 | ✓ |
| c | c | – | d(c,c) + d(c,-) ≥ d(c,-) | dc(c1,c2) + 0.75 ≥ 0.75 | dc(c1,c2) ≥ 0.0 | ✓ |
| c | v | c | d(c,v) + d(v,c) ≥ d(c,c) | 1.0 + 1.0 ≥ dc(c1,c3) | 2.0 ≥ dc(c1,c3) | ✓ |
| c | v | v | d(c,v) + d(v,v) ≥ d(c,v) | 1.0 + dv(v2,v3) ≥ 1.0 | dv(v2,v3) ≥ 0.0 | ✓ |
| c | v | – | d(c,v) + d(v,-) ≥ d(c,-) | 1.0 + 0.75 ≥ 0.75 | 1.75 ≥ 0.75 | ✓ |
| c | – | c | d(c,-) + d(-,c) ≥ d(c,c) | 0.75 + 0.75 ≥ dc(c1,c3) | 1.5 ≥ dc(c1,c3) | ✓ |
| c | – | v | d(c,-) + d(-,v) ≥ d(c,v) | 0.75 + 0.75 ≥ 1.0 | 1.5 ≥ 1.0 | ✓ |
| c | – | – | d(c,-) + d(-,-) ≥ d(c,-) | 0.75 + 0.0 ≥ 0.75 | 0.75 ≥ 0.75 | ✓ |
| v | c | c | d(v,c) + d(c,c) ≥ d(v,c) | 1.0 + dc(c2,c3) ≥ 1.0 | dc(c2,c3) ≥ 0.0 | ✓ |
| v | c | v | d(v,c) + d(c,v) ≥ d(v,v) | 1.0 + 1.0 ≥ dv(v1,v3) | 2.0 ≥ dv(v1,v3) | ✓ |
| v | c | – | d(v,c) + d(c,-) ≥ d(v,-) | 1.0 + 0.75 ≥ 0.75 | 1.75 ≥ 0.75 | ✓ |
| v | v | c | d(v,v) + d(v,c) ≥ d(v,c) | dv(v1,v2) + 1.0 ≥ 1.0 | dv(v1,v2) ≥ 0.0 | ✓ |
| v | v | v | d(v,v) + d(v,v) ≥ d(v,v) | dv(v1,v2) + dv(v2,v3) ≥ dv(v1,v3) | dv(v1,v2) + dv(v2,v3) ≥ dv(v1,v3) | ✓ |
| v | v | – | d(v,v) + d(v,-) ≥ d(v,-) | dv(v1,v2) + 0.75 ≥ 0.75 | dv(v1,v2) ≥ 0.0 | ✓ |
| v | – | c | d(v,-) + d(-,c) ≥ d(v,c) | 0.75 + 0.75 ≥ 1.0 | 1.5 ≥ 1.0 | ✓ |
| v | – | v | d(v,-) + d(-,v) ≥ d(v,v) | 0.75 + 0.75 ≥ dv(v1,v3) | 1.5 ≥ dv(v1,v3) | ✓ |
| v | – | – | d(v,-) + d(-,-) ≥ d(v,-) | 0.75 + 0.0 ≥ 0.75 | 0.75 ≥ 0.75 | ✓ |
| – | c | c | d(-,c) + d(c,c) ≥ d(-,c) | 0.75 + dc(c2,c3) ≥ 0.75 | dc(c2,c3) ≥ 0.0 | ✓ |
| – | c | v | d(-,c) + d(c,v) ≥ d(-,v) | 0.75 + 1.0 ≥ 0.75 | 1.75 ≥ 0.75 | ✓ |
| – | c | – | d(-,c) + d(c,-) ≥ d(-,-) | 0.75 + 0.75 ≥ 0.0 | 1.5 ≥ 0.0 | ✓ |
| – | v | c | d(-,v) + d(v,c) ≥ d(-,c) | 0.75 + 1.0 ≥ 0.75 | 1.75 ≥ 0.75 | ✓ |
| – | v | v | d(-,v) + d(v,v) ≥ d(-,v) | 0.75 + dv(v2,v3) ≥ 0.75 | dv(v2,v3) ≥ 0.0 | ✓ |
| – | v | – | d(-,v) + d(v,-) ≥ d(-,-) | 0.75 + 0.75 ≥ 0.0 | 1.5 ≥ 0.0 | ✓ |
| – | – | c | d(-,-) + d(-,c) ≥ d(-,c) | 0.0 + 0.75 ≥ 0.75 | 0.75 ≥ 0.75 | ✓ |
| – | – | v | d(-,-) + d(-,v) ≥ d(-,v) | 0.0 + 0.75 ≥ 0.75 | 0.75 ≥ 0.75 | ✓ |
| – | – | – | d(-,-) + d(-,-) ≥ d(-,-) | 0.0 + 0.0 ≥ 0.0 | 0.0 ≥ 0.0 | ✓ |
Table 4 Confirmation of the distance triangle rule for phoneme pairs
We now need to determine distances for pairs of consonants, dc(c1,c2), and pairs of vowels, dv(v1,v2). To maintain consistency with the distance criteria and conditions above dc and dv will need to:
- fall in the range 0 to 1 (inclusive)
- have a mean (average) of 0.5
- comply with the distance function conditions 1-4 above
To achieve this we will first develop a relative distance measure for pairs of consonants, and pairs of vowels, that comply with the distance function conditions. Their numeric values will then be uniformly adjusted so they have a range between 0 and 1, and have a mean of 0.5.
Phonetic Distance between Consonants (dc) and Vowels (dv)
Determining the relative distance between two consonants or two vowels is somewhat subjective. There is research that actual attempts to measure this directly through experimentation, for example Patterns of English phoneme confusions by native and non-native listeners – Cutler, Weber, Smits and Cooper 2004.
There are also many reference to metrics or features associated with consonants and vowels. For consonants it is common to associate them with various phonetic articulation features. For vowels it is usual to consider tongue position and lip roundness.
For this analysis we are going to use consonant features and vowel metrics to infer a numeric distance. For consonants, we assume the more features they have in common the closer they are, and conversely, the fewer features they share the further they are apart. For vowels, we will assume the more similar their tongue position and roundness, the closer they are.
Consonant Distance
Table 5 below is an example of the features associated with each consonant:
| Feature | B | CH | D | DH | F | G | HH | JH | K | L | M | N | NG | P | R | S | SH | T | TH | V | W | Y | Z | ZH |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Affricate | ✓ | ✓ | ||||||||||||||||||||||
| Alveolar | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| Dental | ✓ | ✓ | ||||||||||||||||||||||
| Fricative | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||
| Glide | ✓ | ✓ | ||||||||||||||||||||||
| Glottal | ✓ | |||||||||||||||||||||||
| Labial | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| Liquid | ✓ | ✓ | ||||||||||||||||||||||
| Nasal | ✓ | ✓ | ✓ | |||||||||||||||||||||
| Palatal | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||||||||
| Stop | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||||||||
| Velar | ✓ | ✓ | ✓ | |||||||||||||||||||||
| Voiced | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| Voiceless | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Table 5 Consonant features
There are various ways to turn this feature table into a distance measure but to maintain our distance analogy we will treat each feature as a dimension in a multi-dimensional space. A consonant’s coordinates in this space are set to one or zero depending on whether the consonant possesses that feature or not. We can scale each dimension by applying a weight or scaling factor. This provides a way to vary the relative importance of each feature and tune the distance values. Note scaling individual dimensions does not invalidate the distance conditions discussed above.
The distance between two consonants is calculated using the standard Euclidean distance function (in ℝn space):
| d(x,y) = √(w1(x1-y1)2 + w2(x2-y2)2 + … + wn(xn-yn)2) |
| where: |
| xi = 1 when consonant x has feature i, and, 0 when it doesn’t |
| yi = 1 when consonant y has feature i, and, 0 when it doesn’t |
| wi = weight or scaling factor for the ith feature dimension |
The weights (wi) can be adjusted to normalise the resulting distances so that they fall within the range 0-1 and have a mean of 0.5. For those interested in the normalisation method see Appendix A. The result is the following consonant distance (dc) table:
| c1/c2 | B | CH | D | DH | F | G | HH | JH | K | L | M | N | NG | P | R | S | SH | T | TH | V | W | Y | Z | ZH |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 0.00 | 0.58 | 0.25 | 0.52 | 0.30 | 0.35 | 0.91 | 0.54 | 0.40 | 0.53 | 0.35 | 0.43 | 0.50 | 0.20 | 0.54 | 0.39 | 0.40 | 0.32 | 0.56 | 0.23 | 0.47 | 0.50 | 0.34 | 0.35 |
| CH | 0.58 | 0.00 | 0.58 | 0.69 | 0.53 | 0.63 | 0.98 | 0.20 | 0.60 | 0.70 | 0.63 | 0.63 | 0.68 | 0.54 | 0.65 | 0.53 | 0.46 | 0.54 | 0.66 | 0.57 | 0.70 | 0.68 | 0.57 | 0.50 |
| D | 0.25 | 0.58 | 0.00 | 0.52 | 0.39 | 0.35 | 0.91 | 0.54 | 0.40 | 0.47 | 0.43 | 0.35 | 0.50 | 0.32 | 0.54 | 0.30 | 0.40 | 0.20 | 0.56 | 0.34 | 0.53 | 0.50 | 0.23 | 0.35 |
| DH | 0.52 | 0.69 | 0.52 | 0.00 | 0.51 | 0.58 | 0.97 | 0.66 | 0.61 | 0.66 | 0.58 | 0.58 | 0.63 | 0.56 | 0.66 | 0.51 | 0.52 | 0.56 | 0.20 | 0.47 | 0.66 | 0.63 | 0.47 | 0.48 |
| F | 0.30 | 0.53 | 0.39 | 0.51 | 0.00 | 0.46 | 0.86 | 0.57 | 0.42 | 0.56 | 0.39 | 0.46 | 0.52 | 0.23 | 0.57 | 0.25 | 0.27 | 0.34 | 0.47 | 0.20 | 0.50 | 0.53 | 0.32 | 0.33 |
| G | 0.35 | 0.63 | 0.35 | 0.58 | 0.46 | 0.00 | 0.94 | 0.60 | 0.20 | 0.59 | 0.50 | 0.50 | 0.35 | 0.40 | 0.60 | 0.46 | 0.47 | 0.40 | 0.61 | 0.42 | 0.59 | 0.56 | 0.42 | 0.43 |
| HH | 0.91 | 0.98 | 0.91 | 0.97 | 0.86 | 0.94 | 0.00 | 1.00 | 0.92 | 1.00 | 0.94 | 0.94 | 0.98 | 0.89 | 1.00 | 0.86 | 0.87 | 0.89 | 0.95 | 0.88 | 1.00 | 0.98 | 0.88 | 0.89 |
| JH | 0.54 | 0.20 | 0.54 | 0.66 | 0.57 | 0.60 | 1.00 | 0.00 | 0.63 | 0.67 | 0.60 | 0.60 | 0.65 | 0.58 | 0.62 | 0.57 | 0.50 | 0.58 | 0.69 | 0.53 | 0.67 | 0.65 | 0.53 | 0.46 |
| K | 0.40 | 0.60 | 0.40 | 0.61 | 0.42 | 0.20 | 0.92 | 0.63 | 0.00 | 0.62 | 0.54 | 0.54 | 0.40 | 0.35 | 0.63 | 0.42 | 0.43 | 0.35 | 0.58 | 0.46 | 0.62 | 0.60 | 0.46 | 0.47 |
| L | 0.53 | 0.70 | 0.47 | 0.66 | 0.56 | 0.59 | 1.00 | 0.67 | 0.62 | 0.00 | 0.59 | 0.53 | 0.64 | 0.57 | 0.27 | 0.50 | 0.57 | 0.51 | 0.69 | 0.52 | 0.67 | 0.64 | 0.46 | 0.53 |
| M | 0.35 | 0.63 | 0.43 | 0.58 | 0.39 | 0.50 | 0.94 | 0.60 | 0.54 | 0.59 | 0.00 | 0.25 | 0.35 | 0.40 | 0.60 | 0.46 | 0.47 | 0.47 | 0.61 | 0.34 | 0.53 | 0.56 | 0.42 | 0.43 |
| N | 0.43 | 0.63 | 0.35 | 0.58 | 0.46 | 0.50 | 0.94 | 0.60 | 0.54 | 0.53 | 0.25 | 0.00 | 0.35 | 0.47 | 0.60 | 0.39 | 0.47 | 0.40 | 0.61 | 0.42 | 0.59 | 0.56 | 0.34 | 0.43 |
| NG | 0.50 | 0.68 | 0.50 | 0.63 | 0.52 | 0.35 | 0.98 | 0.65 | 0.40 | 0.64 | 0.35 | 0.35 | 0.00 | 0.54 | 0.65 | 0.52 | 0.53 | 0.54 | 0.66 | 0.49 | 0.64 | 0.61 | 0.49 | 0.49 |
| P | 0.20 | 0.54 | 0.32 | 0.56 | 0.23 | 0.40 | 0.89 | 0.58 | 0.35 | 0.57 | 0.40 | 0.47 | 0.54 | 0.00 | 0.58 | 0.34 | 0.35 | 0.25 | 0.52 | 0.30 | 0.51 | 0.54 | 0.39 | 0.40 |
| R | 0.54 | 0.65 | 0.54 | 0.66 | 0.57 | 0.60 | 1.00 | 0.62 | 0.63 | 0.27 | 0.60 | 0.60 | 0.65 | 0.58 | 0.00 | 0.57 | 0.50 | 0.58 | 0.69 | 0.53 | 0.67 | 0.65 | 0.53 | 0.46 |
| S | 0.39 | 0.53 | 0.30 | 0.51 | 0.25 | 0.46 | 0.86 | 0.57 | 0.42 | 0.50 | 0.46 | 0.39 | 0.52 | 0.34 | 0.57 | 0.00 | 0.27 | 0.23 | 0.47 | 0.32 | 0.56 | 0.53 | 0.20 | 0.33 |
| SH | 0.40 | 0.46 | 0.40 | 0.52 | 0.27 | 0.47 | 0.87 | 0.50 | 0.43 | 0.57 | 0.47 | 0.47 | 0.53 | 0.35 | 0.50 | 0.27 | 0.00 | 0.35 | 0.48 | 0.33 | 0.57 | 0.54 | 0.33 | 0.20 |
| T | 0.32 | 0.54 | 0.20 | 0.56 | 0.34 | 0.40 | 0.89 | 0.58 | 0.35 | 0.51 | 0.47 | 0.40 | 0.54 | 0.25 | 0.58 | 0.23 | 0.35 | 0.00 | 0.52 | 0.39 | 0.57 | 0.54 | 0.30 | 0.40 |
| TH | 0.56 | 0.66 | 0.56 | 0.20 | 0.47 | 0.61 | 0.95 | 0.69 | 0.58 | 0.69 | 0.61 | 0.61 | 0.66 | 0.52 | 0.69 | 0.47 | 0.48 | 0.52 | 0.00 | 0.51 | 0.69 | 0.66 | 0.51 | 0.52 |
| V | 0.23 | 0.57 | 0.34 | 0.47 | 0.20 | 0.42 | 0.88 | 0.53 | 0.46 | 0.52 | 0.34 | 0.42 | 0.49 | 0.30 | 0.53 | 0.32 | 0.33 | 0.39 | 0.51 | 0.00 | 0.46 | 0.49 | 0.25 | 0.27 |
| W | 0.47 | 0.70 | 0.53 | 0.66 | 0.50 | 0.59 | 1.00 | 0.67 | 0.62 | 0.67 | 0.53 | 0.59 | 0.64 | 0.51 | 0.67 | 0.56 | 0.57 | 0.57 | 0.69 | 0.46 | 0.00 | 0.18 | 0.52 | 0.53 |
| Y | 0.50 | 0.68 | 0.50 | 0.63 | 0.53 | 0.56 | 0.98 | 0.65 | 0.60 | 0.64 | 0.56 | 0.56 | 0.61 | 0.54 | 0.65 | 0.53 | 0.54 | 0.54 | 0.66 | 0.49 | 0.18 | 0.00 | 0.49 | 0.50 |
| Z | 0.34 | 0.57 | 0.23 | 0.47 | 0.32 | 0.42 | 0.88 | 0.53 | 0.46 | 0.46 | 0.42 | 0.34 | 0.49 | 0.39 | 0.53 | 0.20 | 0.33 | 0.30 | 0.51 | 0.25 | 0.52 | 0.49 | 0.00 | 0.27 |
| ZH | 0.35 | 0.50 | 0.35 | 0.48 | 0.33 | 0.43 | 0.89 | 0.46 | 0.47 | 0.53 | 0.43 | 0.43 | 0.49 | 0.40 | 0.46 | 0.33 | 0.20 | 0.40 | 0.52 | 0.27 | 0.53 | 0.50 | 0.27 | 0.00 |
Table 6 Consonant Distance (dc) Table
Table 6 can be downloaded in csv form here.
Vowel Distance
A similar approach can be applied to vowels only in this case the feature set is replaced with vowel metrics as discussed above. There are many metrics for vowels but we will focus on the three main ones:
- Openness (aka height)
- Backness (aka advance)
- Roundness
There is no exact value for these and they typically vary with different dialects. Here we will assign a value between zero and one for each metric for each vowel based on various vowel charts (see Table 7 below).
There is a further complication with vowels as they come in two main types:
- Pure vowels or monophthongs (EH, IH, AA, UW, AE, AH, ER, AO, IY, UH)
- Diphthongs (EY, AY, OW, AW, OY)
Pure vowels (monophthongs) are similar to consonants in that they have a single set of metric values. In contracts, diphthongs are a combination of two vowel sounds. They commence at one sound and end on another. Monophthongs can be thought of as points in the metric space, whereas diphthongs are line segments. Some of the diphthong starting and ending points are existing monophthongs but others are separate points not corresponding with any existing monophthong.
Table 7 below shows typical monophthongs vowel metrics derived from various sources. It includes three additional “virtual” monophthongs (DA, DE and DO) used by the diphthongs:
| Vowel | Openness | Backness | Roundness | Example |
|---|---|---|---|---|
| AA | 1.00 | 1.00 | 0.00 | pot, odd, balm |
| AE | 0.80 | 0.40 | 0.00 | trap, bad |
| AH | 0.70 | 1.00 | 0.00 | strut, mud, love, blood |
| AO | 0.70 | 1.00 | 1.00 | thought, law, north, war |
| DA | 1.00 | 0.50 | 0.00 | (start point for diphthong AY, AW) |
| DE | 0.30 | 0.20 | 0.00 | (start point for diphthong EY) |
| DO | 0.30 | 1.00 | 1.00 | (start point for diphthong OW) |
| EH | 0.70 | 0.40 | 0.00 | dress, bed, head, many |
| ER | 0.70 | 0.60 | 0.00 | nurse, stir, learn, refer |
| IH | 0.20 | 0.30 | 0.00 | kit, bid, hymn, minute |
| IY | 0.00 | 0.00 | 0.00 | fleece, sea, machine |
| UH | 0.20 | 0.80 | 1.00 | foot, good, put |
| UW | 0.00 | 1.00 | 1.00 | goose, two, blue, group |
Table 7 Pure vowel (monophthong) metric data
As with consonants, the distance between two monophthong vowels is calculated using the standard Euclidean distance function:
| d(x,y) = √(wo(xo-yo)2 + wb(xb-yb)2 + wr(xr-yr)2) |
| where: |
| wo, xo, yo are the openness weight, x and y respectively |
| wb, xb, yb are the backness weight, x and y respectively |
| wr, xr, yr are the roundness weight, x and y respectively |
The weights can be adjusted, in the same way as the consonants, to normalise the result (see Appendix A). Table 8 below shows the resulting monophthong vowel distances:
| v1/v2 | AA | AE | AH | AO | DA | DE | DO | EH | ER | IH | IY | UH | UW |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AA | 0.00 | 0.45 | 0.21 | 0.49 | 0.35 | 0.75 | 0.66 | 0.47 | 0.35 | 0.75 | 1.00 | 0.73 | 0.83 |
| AE | 0.45 | 0.00 | 0.43 | 0.62 | 0.16 | 0.38 | 0.71 | 0.07 | 0.16 | 0.43 | 0.63 | 0.68 | 0.83 |
| AH | 0.21 | 0.43 | 0.00 | 0.44 | 0.41 | 0.63 | 0.53 | 0.42 | 0.28 | 0.61 | 0.86 | 0.58 | 0.66 |
| AO | 0.49 | 0.62 | 0.44 | 0.00 | 0.61 | 0.77 | 0.28 | 0.61 | 0.53 | 0.75 | 0.97 | 0.38 | 0.49 |
| DA | 0.35 | 0.16 | 0.41 | 0.61 | 0.00 | 0.54 | 0.75 | 0.22 | 0.22 | 0.58 | 0.79 | 0.75 | 0.91 |
| DE | 0.75 | 0.38 | 0.63 | 0.77 | 0.54 | 0.00 | 0.72 | 0.32 | 0.40 | 0.10 | 0.25 | 0.62 | 0.75 |
| DO | 0.66 | 0.71 | 0.53 | 0.28 | 0.75 | 0.72 | 0.00 | 0.68 | 0.60 | 0.67 | 0.86 | 0.16 | 0.21 |
| EH | 0.47 | 0.07 | 0.42 | 0.61 | 0.22 | 0.32 | 0.68 | 0.00 | 0.14 | 0.36 | 0.57 | 0.63 | 0.79 |
| ER | 0.35 | 0.16 | 0.28 | 0.53 | 0.22 | 0.40 | 0.60 | 0.14 | 0.00 | 0.41 | 0.65 | 0.58 | 0.72 |
| IH | 0.75 | 0.43 | 0.61 | 0.75 | 0.58 | 0.10 | 0.67 | 0.36 | 0.41 | 0.00 | 0.25 | 0.57 | 0.68 |
| IY | 1.00 | 0.63 | 0.86 | 0.97 | 0.79 | 0.25 | 0.86 | 0.57 | 0.65 | 0.25 | 0.00 | 0.73 | 0.83 |
| UH | 0.73 | 0.68 | 0.58 | 0.38 | 0.75 | 0.62 | 0.16 | 0.63 | 0.58 | 0.57 | 0.73 | 0.00 | 0.20 |
| UW | 0.83 | 0.83 | 0.66 | 0.49 | 0.91 | 0.75 | 0.21 | 0.79 | 0.72 | 0.68 | 0.83 | 0.20 | 0.00 |
Table 8 Pure vowel (monophthong) distance table
To accommodate the diphthongs we begin with their starting and ending monophthongs as shown below:
| Diphthong | Start vowel | End vowel | Examples |
|---|---|---|---|
| EY | DE | IH | face, day, break |
| AY | DA | IH | price, high, try |
| OW | DO | UH | goat, show, no |
| AW | DA | UH | mouth, now |
| OY | AO | IH | choice, boy |
Table 9 Diphthong starting and ending monophthongs
A natural way to handle diphthongs is to treat them as a straight line trajectory from the first vowel to the second vowel. This makes them a straight line segment in the metric space. To incorporate diphthongs into the vowel distance table we determine the average distance from a monophthong point to a diphthong line segment or the average distance from a diphthong line segment to another diphthong line segment.
These averages can be calculated either numerically, by assigning a (large) number of points over the line segment, or segments, calculating the distance to each point and averaging the result, or analytically, by defining the distance in terms of a variable and integrating (see Appendix B for details).
After adding the monophthong-to-diphthong and diphthong-to-diphthong distances, and removing the virtual diphthong vowels (DA, DE and DO) the final combined vowel table is:
| v1/v2 | AA | AE | AH | AO | AW | AY | EH | ER | EY | IH | IY | OW | OY | UH | UW |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AA | 0.00 | 0.45 | 0.21 | 0.49 | 0.47 | 0.52 | 0.47 | 0.35 | 0.75 | 0.75 | 1.00 | 0.70 | 0.55 | 0.73 | 0.83 |
| AE | 0.45 | 0.00 | 0.43 | 0.62 | 0.34 | 0.18 | 0.07 | 0.16 | 0.40 | 0.43 | 0.63 | 0.69 | 0.43 | 0.68 | 0.83 |
| AH | 0.21 | 0.43 | 0.00 | 0.44 | 0.40 | 0.46 | 0.42 | 0.28 | 0.62 | 0.61 | 0.86 | 0.55 | 0.43 | 0.58 | 0.66 |
| AO | 0.49 | 0.62 | 0.44 | 0.00 | 0.39 | 0.64 | 0.61 | 0.53 | 0.76 | 0.75 | 0.97 | 0.33 | 0.38 | 0.38 | 0.49 |
| AW | 0.47 | 0.34 | 0.40 | 0.39 | 0.00 | 0.28 | 0.33 | 0.29 | 0.48 | 0.49 | 0.70 | 0.38 | 0.32 | 0.37 | 0.54 |
| AY | 0.52 | 0.18 | 0.46 | 0.64 | 0.28 | 0.00 | 0.16 | 0.21 | 0.27 | 0.29 | 0.51 | 0.63 | 0.30 | 0.62 | 0.76 |
| EH | 0.47 | 0.07 | 0.42 | 0.61 | 0.33 | 0.16 | 0.00 | 0.14 | 0.34 | 0.36 | 0.57 | 0.65 | 0.39 | 0.63 | 0.79 |
| ER | 0.35 | 0.16 | 0.28 | 0.53 | 0.29 | 0.21 | 0.14 | 0.00 | 0.40 | 0.41 | 0.65 | 0.59 | 0.35 | 0.58 | 0.72 |
| EY | 0.75 | 0.40 | 0.62 | 0.76 | 0.48 | 0.27 | 0.34 | 0.40 | 0.00 | 0.05 | 0.25 | 0.64 | 0.39 | 0.59 | 0.71 |
| IH | 0.75 | 0.43 | 0.61 | 0.75 | 0.49 | 0.29 | 0.36 | 0.41 | 0.05 | 0.00 | 0.25 | 0.62 | 0.38 | 0.57 | 0.68 |
| IY | 1.00 | 0.63 | 0.86 | 0.97 | 0.70 | 0.51 | 0.57 | 0.65 | 0.25 | 0.25 | 0.00 | 0.80 | 0.60 | 0.73 | 0.83 |
| OW | 0.70 | 0.69 | 0.55 | 0.33 | 0.38 | 0.63 | 0.65 | 0.59 | 0.64 | 0.62 | 0.80 | 0.00 | 0.35 | 0.08 | 0.20 |
| OY | 0.55 | 0.43 | 0.43 | 0.38 | 0.32 | 0.30 | 0.39 | 0.35 | 0.39 | 0.38 | 0.60 | 0.35 | 0.00 | 0.36 | 0.50 |
| UH | 0.73 | 0.68 | 0.58 | 0.38 | 0.37 | 0.62 | 0.63 | 0.58 | 0.59 | 0.57 | 0.73 | 0.08 | 0.36 | 0.00 | 0.20 |
| UW | 0.83 | 0.83 | 0.66 | 0.49 | 0.54 | 0.76 | 0.79 | 0.72 | 0.71 | 0.68 | 0.83 | 0.20 | 0.50 | 0.20 | 0.00 |
Table 10 Combined monophthong and diphthong vowel distance table
Table 10 can be downloaded in csv form here.
Phoneme Duration
By their nature phonemes vary in duration. Their duration can be determined from experimental data. The duration times in Table 11 below are based data from Andras Kornai’s FORMAL PHONOLOGY.
For our purposes the duration times, measured in milliseconds, need to be converted into a number of repeated phonemes that reflect these times. Somewhat arbitrarily, a range from 5 to 15 repeats has been selected and the durations time have been “compressed” into this range to determine the repeats associated with each phoneme.
Vowels have three values for the three stress cases (p = Primary, s = Secondary and n = No stress). These were determined by making the the primary stress 20% greater, and no stress 20% less, than the secondary stress which took its base duration from the above reference. Repeats have been rounded to the nearest integer.
|
|
Table 11 Phoneme durations and repeats
One further refinement is to increase the duration of the final phoneme of a word if it is a vowel. There is a tendency to linger on the final vowel sound especially when the word is said in isolation. For example, consider the length of the “o” when saying “echo chamber” versus “echo” by itself. To accommodate this phenomenon the repeats of a final vowel are increased by 20%.
Word Distance
By combining the elements above, we are finally in a position to determine the phonetic distance between two arbitrary words using the following process:
- Convert each word into a string of phonemes (using the CMU dictionary)
- Repeat each phoneme in the string the number of times associated with it’s duration (table above)
- Convolute the two strings and calculate the result using the vowel/consonant/null phoneme distance tables (see Appendix C for details on coding discrete convolution)
- Take the minimum value of the convolution as the phonetic distance between the two words
This will produce a raw distance value. As a simple example consider the distance between “cat” and “mouse”.
1. Convert to phonemes:
cat -> K AE1 T
mouse -> M AW1 S
2. Repeat phonemes based on their duration (vowel stress numbers removed for brevity)
cat -> K K K K K K K K K AE AE AE AE AE AE AE AE AE AE AE AE T T T T T T T T
mouse -> M M M M M M M AW AW AW AW AW AW AW AW AW AW AW AW AW AW AW S S S S S S S S S
3. Calculate the distance value for each case as the two strings "pass over" each other
... - - - - - - - - - - - - - K K K K K K K K K AE AE AE AE ...
... AW AW AW AW AW S S S S S S S S S
... - - - - - - - - - - - - - K K K K K K K K K AE AE AE AE ...
... AW AW AW AW AW AW S S S S S S S S S
... - - - - - - - - - - - - - K K K K K K K K K AE AE AE AE ...
... AW AW AW AW AW AW AW S S S S S S S S S
:
:
- K K K K K K K K K AE AE AE AE AE AE AE AE AE AE AE AE T T T T T T T T -
M M M M M M M AW AW AW AW AW AW AW AW AW AW AW AW AW AW AW S S S S S S S S S
K K K K K K K K K AE AE AE AE AE AE AE AE AE AE AE AE T T T T T T T T - -
M M M M M M M AW AW AW AW AW AW AW AW AW AW AW AW AW AW AW S S S S S S S S S
K K K K K K K K K AE AE AE AE AE AE AE AE AE AE AE AE T T T T T T T T - - -
- M M M M M M M AW AW AW AW AW AW AW AW AW AW AW AW AW AW AW S S S S S S S S S
:
:
... AE AE AE AE AE AE T T T T T T T T - - - - - - - - - - - - - - - - ...
... - - - - - - - - - - - - - M M M M M M M AW AW AW AW AW AW AW AW AW AW...
4. Select the smallest distance
The raw phonetic distance is not that useful as it is always possible to increase it by using longer words with more phonemes. The distance per phoneme is a more useful measure as it focuses on the distance between the phonemes themselves by discounting the length of the words.
However, for our purposes, we want to go one step further by imposing a cost on the length of words. That is, we want the greatest distance for the shortest words. So we can define a relative phonetic distance between two words (w1 and w2) as the raw phonetic distance divided by the average number of phonemes raise to some power λ (lambda for length sensitivity).
| rel-distλ(w1,w2) = raw-dist(w1,w2) / avg-ph-cnt(w1,w2)λ |
| where: |
| rel-distλ(w1,w2) = relative distance between w1 and w2 for λ ≥ 0 |
| raw-dist = raw distance between w1 and w2 |
| avg-ph-cnt = average number of phonemes in w1 and w2 |
Note when λ = 0, rel-dist = raw-dist, and when λ = 1, rel-dist = raw-dist / avg-ph-cnt = raw-dist per phoneme. For high values of λ the relative distance is increasingly penalised (reduced) by the length of the words. This gives us a way to tune the relative distance to reflect how expensive word length is to the outcome.
To see how these measures work in practice, consider the following example comparing the relative phonetic distances between the word ‘cat’ and some other sample words. The number of phonemes in each word is shown in parentheses () after the word. The numbers in brackets [] after the distances are their order, or rank, (1=largest, 2=next largest, etc) within the column.
| Word 1 | Word 2 | λ=0 | λ=1 | λ=1.5 | λ=2 | λ=2.5 | λ=3 |
|---|---|---|---|---|---|---|---|
| cat (3) | cat (3) | 0.00 [6] | 0.00 [6] | 0.00 [6] | 0.00 [6] | 0.00 [6] | 0.00 [6] |
| cat (3) | mat (3) | 5.25 [5] | 1.75 [5] | 1.01 [5] | 0.58 [5] | 0.34 [5] | 0.19 [3] |
| cat (3) | dog (3) | 14.63 [4] | 4.88 [3] | 2.82 [2] | 1.63 [1] | 0.94 [1] | 0.54 [1] |
| cat (3) | dogs (4) | 17.78 [3] | 5.08 [2] | 2.72 [3] | 1.45 [2] | 0.78 [2] | 0.41 [2] |
| cat (3) | catalog (7) | 24.00 [2] | 4.80 [4] | 2.15 [4] | 0.96 [4] | 0.43 [4] | 0.19 [4] |
| cat (3) | university (10) | 49.98 [1] | 7.69 [1] | 3.02 [1] | 1.18 [3] | 0.46 [3] | 0.18 [5] |
Table 12 Relative word distance for various λ values (with rank indicator)
This example confirms what we might expect from the distance measures considered so far:
- Distance between “cat” and “cat” is zero (as would be expected)
- Word pairs with more phonemes have larger raw distances (λ=0)
- Relative distances place more emphasis on word lengths as λ increases. For example, “dog” goes from rank 4 to rank 1, and, “university” goes from rank 1 to rank 5 as λ increases from 0 to 3.
Another way to view this is to plot the relative distance of each word from “cat” (excluding “cat” itself) against λ. The plot in Figure 1 below uses a log scale to improve clarity. It shows how the longer words start with larger values but reduce more quickly as λ increases. Note also that words with the same phoneme count, such as “mat” and “dog” maintain their relative difference regardless of the value of λ.
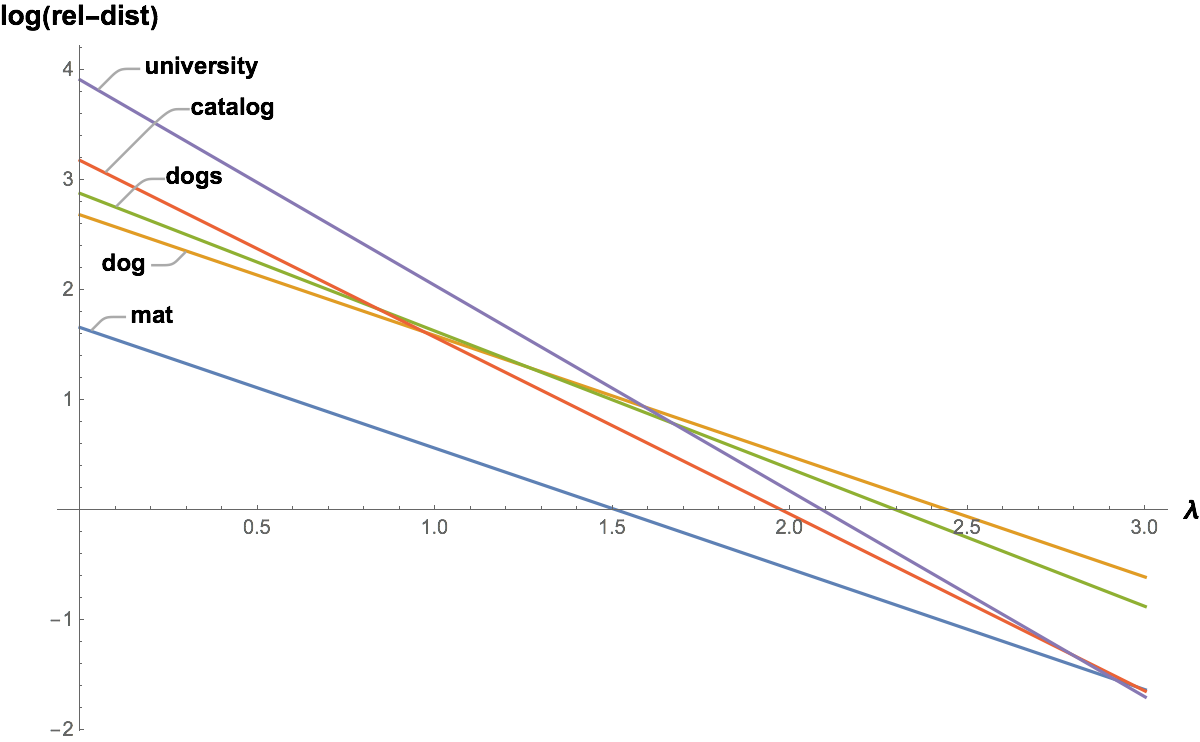
Figure 1 Relative distance (log scale) from “cat” versus λ for some sample words
We can extend these ideas to groups of words instead of just pairs.
Word Groups
Before looking at ways to compare different groups of words, we should explicitly state two underlying assumptions we will use:
- The greater the phonetic distance (as described above) between two words, the less likely they are to be confused
- The number of phonemes in a word is a reasonable measure of the ‘cost’ of using (saying) the word
The first is the basis of the work above. We have implicitly assumed that the more differences in consonant features, vowel metrics and duration between words, the less likely the words will be confused. We can partly confirm this by our own experiences and partly by common sense. In reality, it is likely the degree of confusion between words is more nuanced, and shrouded in how our brains process and recognise sounds. However, for our purposes, the approach taken will have to suffice.
The second assumption is more straightforward. Although there are differences in the duration of individual phonemes, these tend to average out within a words. Further the transition between each phoneme also affects the duration of pronouncing the word. So the number of phonemes in a word is a reasonable measure of the cost associated with its reproduction.
Armed with these two assumptions, we can perform a cost/benefit analysis on groups of words. The cost is associated with the phoneme counts of the words, while the benefit is the phonetic separation achieved between them.
As a concrete example, let’s return to the six words used to represent the hexadecimal characters (A-F) discussed earlier.
Hex Words
The two tables below show the raw distance, and relative distance (λ=2), in parentheses, for each hexadecimal word pairings for the ISA and USPA abbreviations respectively.
| ISA | alpha (4) | bravo (5) | charlie (5) | delta (5) | echo (3) | foxtrot (8) |
|---|---|---|---|---|---|---|
| alpha (4) | 0.0 (0.00) | 31.4 (1.55) | 27.9 (1.38) | 11.8 (0.58) | 20.1 (1.64) | 47.3 (1.31) |
| bravo (5) | – | 0.0 (0.00) | 29.9 (1.20) | 28.8 (1.15) | 21.3 (1.33) | 46.4 (1.10) |
| charlie (5) | – | – | 0.0 (0.00) | 28.3 (1.13) | 33.4 (2.09) | 43.7 (1.03) |
| delta (5) | – | – | – | 0.0 (0.00) | 21.9 (1.37) | 46.0 (1.09) |
| echo (3) | – | – | – | – | 0.0 (0.00) | 47.8 (1.58) |
| foxtrot (8) | – | – | – | – | – | 0.0 (0.00) |
Table 13 Raw and relative distance (λ=2) of the ISA hex words
| USPA | able (4) | baker (4) | charlie (5) | dog (3) | easy (3) | fox (4) |
|---|---|---|---|---|---|---|
| able (4) | 0.0 (0.00) | 18.2 (1.14) | 34.0 (1.68) | 24.0 (1.96) | 18.4 (1.50) | 29.4 (1.84) |
| baker (4) | – | 0.0 (0.00) | 34.0 (1.68) | 22.0 (1.79) | 22.0 (1.79) | 23.1 (1.44) |
| charlie (5) | – | – | 0.0 (0.00) | 29.5 (1.85) | 28.2 (1.76) | 22.4 (1.11) |
| dog (3) | – | – | – | 0.0 (0.00) | 26.5 (2.95) | 18.9 (1.54) |
| easy (3) | – | – | – | – | 0.0 (0.00) | 32.2 (2.63) |
| fox (4) | – | – | – | – | – | 0.0 (0.00) |
Table 14 Raw and relative distance (λ=2) of the USPA hex words
The question is how best to compare these two schemes and, indeed, schemes in general?
As suggested above, we want to maximise the benefit/cost ratio (or minimise the cost/benefit ratio) where benefit is some function of distance and cost some function of the number of phonemes. We also may want to consider the frequency or probability of words, that is, how often a word (or its associated letter) occurs. For hexadecimals, and many other real life scenarios (e.g call signs), this is expected to be approximately the same for each letter/word. But in some contexts, particular letter/words may be used more frequently than others.
Cost
Let’s start with the cost side of the equation. As we are assuming the cost is proportional to the number of phonemes in the word, the cost of saying the entire set of words is the sum of the probability (p) multiplied by the phoneme count (c) of each word.
| cost = p1c1 + p2c2 + … + pncn = Σpici |
| where: |
| pi = probability of wordi (or its associated letter) occurring |
| ci = phoneme count for wordi |
| Note: p1 + p2 + … + pn = Σpi = 1 |
When the probability of each word is equally likely, as in the case of hexadecimal letters, pi = 1/n and the cost equation becomes a simple arithmetic mean:
| cost = (1/n)c1 + (1/n)c2 + … + (1/n)cn = Σ(1/n)ci = Σci / n |
This is a simple and effective cost measure. It would be possible to emphasis, and penalise, more costly (longer) words by using the generalised or power mean. It raises each value to some power before summing them. This inflates larger values and increases their relative contribution to the sum (assuming the exponent is greater than one). To normalise the result, the root is taken to the same power as shown below:
| cost = (Σpiciτ)1/τ |
| or for pi = 1/n |
| cost = (Σ(1/n)ciτ)1/τ = (Σciτ/n)1/τ |
| where: |
| τ = constant |
| Note when τ=1, cost = Σci/n (as above) |
However, for our purposes we will stick to the simple arithmetic mean of the phoneme counts.
Benefit
Now let’s consider the benefit side of the equation for a group of words.
If there are n words in the group, each word has n-1 neighbours and n-1 corresponding distances to them. So there is a total of n(n-1)/2 distances between the n words. To simplify matters, we will focus on the distance between a word and its nearest neighbour. This is the minimum distance associate with each word. It can be interpreted as a measure of the likelihood the word will be confused with another. It also means we only need to consider n distances for the benefit equation.
Figure 2 below shows graphs of the ISA and USPA words (nodes) with the links (edges) between them representing the raw distance from the table above. The minimum distance edges for each word are coloured along with their associated nodes (not to scale). It can be seen that the minimum minimum distance (red edge) is always shared between two nodes. While other nodes can either share or have their own minimum distance.
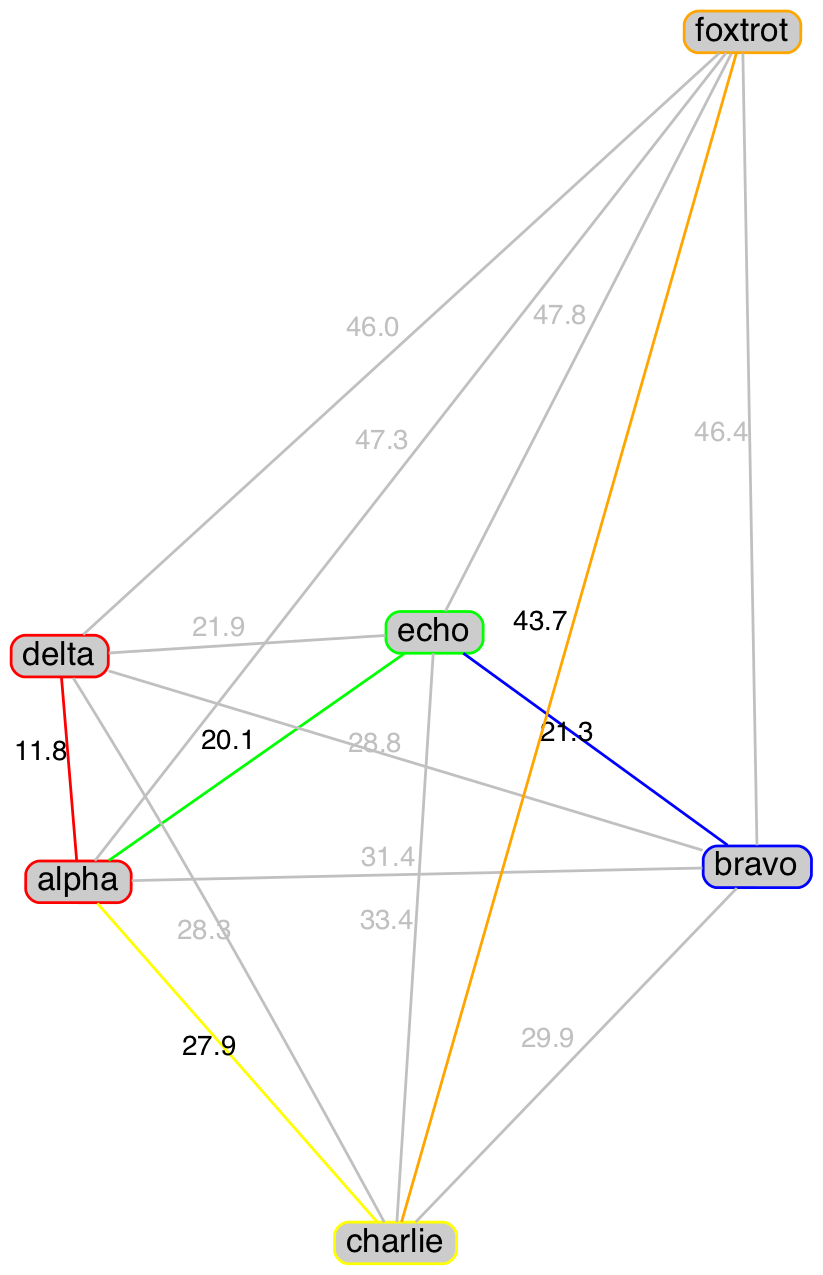 |
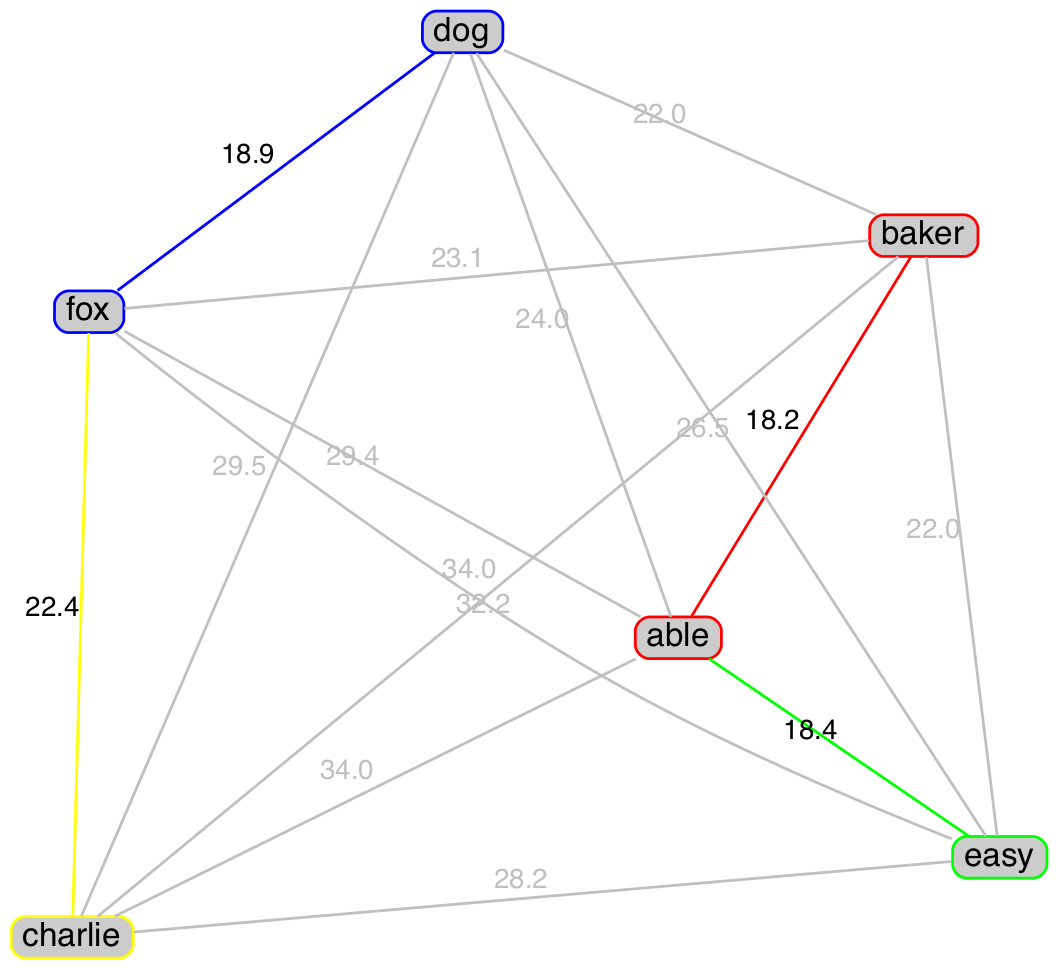 |
Figure 2 Minimum distance between ISA and USPA words
The result of this approach is that each letter/word is assigned a single distance value representing its worst case separation denoted d.
We can treat this minimum distance in a similar way to the cost phoneme count. Again the probability of the word being used can be similarly accommodated.
| benefit = p1d1 + p2d2 + … + pndn = Σpidi |
| or for pi = 1/n |
| benefit = Σdi / n |
| where: |
| pi = probability of wordi (or its associated letter) occurring |
| di = distance between wordi and its nearest neighbour |
| Note: p1 + p2 + … + pn = Σpi = 1 |
Of course there a many other ways the cost and benefit equations could be formulated. There is no “correct” approach, but each should provide similar general results–reducing the cost for shorter words and increasing the benefit for greater separation–with only the quantum varying.
Quality Measure
The ratio of benefit to cost provides a quality measure for a set of words. The better the separation the greater the quality. The shorter the words (few phonemes) the greater the quality. The sensitivity to word length can be tuned with the λ parameters as follows:
| qualλ = Σpidi / (Σpici)λ |
| or for pi = 1/n |
| qualλ = (Σdi/n) / (Σci/n)λ |
To simplify matters we will consider three “special” cases of the quality measure assuming equal likelihood of letters/words:
| qual0 = Σdi/n |
| qual1 = (Σdi/n) / (Σci/n) |
| qual2 = (Σdi/n) / (Σci/n)2 |
The first (qual0) is just the average minimum distance. It takes no account of the length of the words. Some constraint on the word length can be externally imposed by limiting the length of the candidate words available for selection.
The second (qual1) is the average minimum distance per phoneme. It takes basic account of the word length meaning longer words are not necessarily better than shorter ones but it places no particular penalty on longer words.
The last (qual2) places more emphasis on word length by penalising longer words. This is the most useful for our purposes as it represents the most economic measure.
We are now in a position to assess the two hexadecimal scheme above using these quality measures:
| Scheme | avg-phs | qual0 | qual1 | qual2 |
|---|---|---|---|---|
| ISA | 5.00 | 22.76 | 4.55 | 0.91 |
| USPA | 3.83 | 19.18 | 5.00 | 1.31 |
Table 15 Hex word quality comparison
These results show that while the average minimum distance (qual0) for ISA are greater than USPA, USPA improves as λ increases because its average phoneme count is significantly smaller. These figures suggest that for hexadecimal words, at least, USPA is a significantly more economic scheme (by about 44%).
We will look at some alternative hexadecimal schemes later that have even better economy. Before we can create new schemes, however, we need a source of candidate words.
Candidate Words
For each letter of the alphabet we need a set of suitable words to represent it. The words must:
- Start with that letter (i.e. p for pot)
- Sound the letter as expected (i.e. p for pot but not p for physics nor e for europe)
To achieve the second condition, an acceptable first phoneme (or phonemes) is assigned for each letter. The following table show the proposed phoneme mapping.
|
|
Table 16 Initial word phoneme(s) for each letter
Note:
- There can be multiple phonemes to cover the case where a vowel, for example, sounds differently at the beginning of a word, for example, echo (EH) and easy (IY)
- The letter C uses the CH sound (as in check) instead of the K sound (as in cat) to distinguish it from the letter K which uses the K sound (as in kite)
- The letter X is a special case, as it invariably sounds like Z when used at the start of a word (e.g. xenon, xerox and xylophone). The one notable exception is x-ray which perforce will be used for the letter X.
Using the first letter and phonemes listed above we can assign words to letters. However, there are a few challenges in creating an suitable list of candidate words. Many of the words in the CMU are not suitable for various reasons and would make poor candidate words. For example, words that fall into any of the following categories may not be considered suitable:
- Uncommon, obscure, archaic or foreign
- Derogatory, racist, sexist, rude, indecent, swearwords, slang or intimate
- Negative, depressing, anti-social
- Technical or specialist in nature such as anatomical or botanical terms
- Warning or emergency (e.g. fire, help, danger)
- Numbers (e.g. one, two, …)
- Place names such as countries, cities, rivers, etc.
- Personal names (although these can be useful because they are often well known)
- Company names, trademarks or product names (with possible legal implications)
- Non root words (e.g plurals and other derivatives)
- Religious, sacred or iconic
- Abbreviations, acronyms or colloquial terms
- Homonyms and homophones
- Overly short or long words
This list is probably not exhaustive, in short, there are many and varied reasons to exclude words. Perhaps it is easier to define acceptable words as: common simple root words with a neutral or positive character that are unlikely to be offensive or symbolic to most people.
Consideration as to how the words will be used is also important. If they are for ad hoc use, in casual situations without a prior formal agreement, common and familiar words will be more effective. However, if the scheme is going to be used by a formal agreement between parties (e.g. ISA), it is more acceptable to use less common words as they will be familiar and expected by the parties involved. Indeed, somewhat obscure words may even be preferred as they are more readily recognisable as letter substitutes.
The CMU dictionary is full of words that would be caught in the unsuitable categories above. In particular, it has a large number of abbreviations, proper nouns and derivations. So as a more concise and manageable source of words we will use Google 10,000 most common English words as a base source. Of course the Google words also contain many words that fall into the undesirable categories above. As a result, a number of words have been excluded from the Google set to produce a subset for use in the examples below.
Alternative Hexadecimal Word Sets
Can we find alternative hexadecimal word sets to ISA and USPA that produce a higher quality result?
A simple approach would be to try every combination of the words representing the letters A-F and select the combination with the highest quality score. A little thought will reveal this has complexity scaling problems. If we assume about 10,000 / 26 (approx. 385) words per letter, there will be around 3856 or 3.25 x 1015 word combinations to analyse. Searching this entire solution space is problematic even with a fast computer and would be impossible with larger word groups like A-Z for the full alphabet.
Rather than looking for the optimal solution, we can find a sub-optimal, but hopefully still good solution, by reducing the size of the search. One simple approach is to:
- Select a word at random for each letter from the word candidates.
- Order the words from smallest to largest based on their minimum distance (i.e. distance to their nearest neighbour). When this is equal (which always occurs at least once) order by the number of candidate words available, least to most. So select the word with the closest neighbour and least number of alternative words first.
- For the selected word, try replacing it with each of the available alternative words from the candidate words. Calculate the resulting quality measure for the new word set and select the best alternative word based on this measure, or leave the current word if no improved word can be found.
- Repeat the above step for each word in turn.
- If there are no improvement found for any word finish, otherwise loop back to Step 2.
This is a simple form of gradient accent where each dimension (letter/word) is examined in turn for “higher ground”. Once no further improvement can be found we have reached a local maximum. By repeating the process for different random starting points we can search for better local maximums.
Some results from applying this approach to candidate words restricted to 3-5 phonemes using our three quality measures above (qual0, qual1 and qual2) are shown below in Tables 17, 18 and 19 respectively.
Local Maximum λ=0 (Hex35-λ0)
| Hex35-λ0 | april (5) | balloon (5) | charter (5) | donate (5) | energy (5) | frank (5) |
|---|---|---|---|---|---|---|
| april (5) | 0.0 (0.00) | 31.8 (1.27) | 34.4 (1.38) | 34.1 (1.36) | 33.9 (1.35) | 32.3 (1.29) |
| balloon (5) | – | 0.0 (0.00) | 34.5 (1.38) | 30.5 (1.22) | 32.6 (1.30) | 32.2 (1.29) |
| charter (5) | – | – | 0.0 (0.00) | 36.9 (1.47) | 37.4 (1.50) | 33.8 (1.35) |
| donate (5) | – | – | – | 0.0 (0.00) | 32.0 (1.28) | 35.1 (1.40) |
| energy (5) | – | – | – | – | 0.0 (0.00) | 33.7 (1.35) |
| frank (5) | – | – | – | – | – | 0.0 (0.00) |
Table 17 Sample qual0 local maximum for hex words using 3-5 phonemes
Local Maximum λ=1 (Hex35-λ1)
| Hex35-λ1 | april (5) | balloon (5) | charter (5) | donate (5) | energy (5) | frank (5) |
|---|---|---|---|---|---|---|
| april (5) | 0.0 (0.00) | 31.8 (1.27) | 34.4 (1.38) | 34.1 (1.36) | 33.9 (1.35) | 32.3 (1.29) |
| balloon (5) | – | 0.0 (0.00) | 34.5 (1.38) | 30.5 (1.22) | 32.6 (1.30) | 32.2 (1.29) |
| charter (5) | – | – | 0.0 (0.00) | 36.9 (1.47) | 37.4 (1.50) | 33.8 (1.35) |
| donate (5) | – | – | – | 0.0 (0.00) | 32.0 (1.28) | 35.1 (1.40) |
| energy (5) | – | – | – | – | 0.0 (0.00) | 33.7 (1.35) |
| frank (5) | – | – | – | – | – | 0.0 (0.00) |
Table 18 Sample qual1 local maximum for hex words using 3-5 phonemes
Local Maximum λ=2 (Hex35-λ2)
| Hex35-λ2 | april (5) | balloon (5) | charter (5) | donate (5) | energy (5) | frank (5) |
|---|---|---|---|---|---|---|
| april (5) | 0.0 (0.00) | 31.8 (1.27) | 34.4 (1.38) | 34.1 (1.36) | 33.9 (1.35) | 32.3 (1.29) |
| balloon (5) | – | 0.0 (0.00) | 34.5 (1.38) | 30.5 (1.22) | 32.6 (1.30) | 32.2 (1.29) |
| charter (5) | – | – | 0.0 (0.00) | 36.9 (1.47) | 37.4 (1.50) | 33.8 (1.35) |
| donate (5) | – | – | – | 0.0 (0.00) | 32.0 (1.28) | 35.1 (1.40) |
| energy (5) | – | – | – | – | 0.0 (0.00) | 33.7 (1.35) |
| frank (5) | – | – | – | – | – | 0.0 (0.00) |
Table 19 Sample qual2 local maximum for hex words using 3-5 phonemes
The Hex35-λ0 solution optimises for qual0 where word length is ignored, so it only requires maximising the distance between words. Hence the result uses the longest words available – in this case five phonemes.
The Hex35-λ1 solution optimises for qual1, where the distance per phoneme is important, so the word length is essentially irrelevant. As a result we see a variety of word lengths.
Finally for the Hex35-λ2 solution which optimises for qual2, the word length penalises the result more and the solution favours words with the smallest phoneme count (while still trying to maximise separation distances).
Table 20 below compares these three local maximum solutions with the ISA and USPA schemes.
| Scheme | avg-phs | qual0 | qual1 | qual2 |
|---|---|---|---|---|
| ISA | 5.00 | 22.76 | 4.55 | 0.91 |
| USPA | 3.83 | 19.18 | 5.00 | 1.31 |
| Hex35-λ0 | 5.00 | 31.80 | 6.36 | 1.27 |
| Hex35-λ1 | 4.17 | 29.15 | 7.00 | 1.68 |
| Hex35-λ2 | 3.00 | 21.39 | 7.13 | 2.38 |
Table 20 Comparison of ISA, USPA and three local maximum word sets
We can see that the generated solutions deliver significantly better results in their quality category (highlighted cells) than either ISA or USPA. It also highlights that the solution produced using the local maximum procedure above is not necessarily the true maximum solution. The Hex35-λ2 word set is actually a better solution than the Hex35-λ1 word set for the qual1 measure. So Hex35-λ1 is clearly sub-optimal.
These generated word solutions are, of course, only one example of many possible word combinations that also score highly. Listed below is Hex35-λ2 and some other results with high qual2 scores in descending order:
- act, bar, choice, duo, easy, fly (2.38)
- arrow, bug, choice, duo, easy, fly (2.31)
- arrow, booth, choice, dry, easy, far (2.30)
- acre, beach, chuck, duo, end, fly (2.25)
- amy, beach, choice, dry, echo, far (2.24)
- ask, beach, choice, duo, era, fly (2.23)
- annie, blue, choice, dock, east, fill (2.21)
- arrow, bouquet, chase, door, easy, fly (2.15)
- alloy, blue, chief, doll, end, folk (2.12)
Finally, as a baseline of sorts, let’s include a random sample of words with 3-5 phoneme counts. Table 21 below includes the average results (rand-35) of 1000 words sets drawn randomly from the same 3-5 phoneme word pool used by the local maximum solutions.
| Scheme | avg-phs | qual0 | qual1 | qual2 |
|---|---|---|---|---|
| ISA | 5.00 | 22.76 | 4.55 | 0.91 |
| USPA | 3.83 | 19.18 | 5.00 | 1.31 |
| Hex35-λ0 | 5.00 | 31.80 | 6.36 | 1.27 |
| Hex35-λ1 | 4.17 | 29.15 | 7.00 | 1.68 |
| Hex35-λ2 | 3.00 | 21.39 | 7.13 | 2.38 |
| rand-35 | 4.04 | 18.86 | 4.67 | 1.16 |
Table 21 Includes average results from 1000 random samples taken from 3-5 phoneme words
It is interesting to note that for the six hexadecimal letters, ISA scores worse than a random sample on two of the three quality measures. USPA is marginally better on all three. All the constructed word sets score significantly better than the random samples for their optimised measure, and indeed better for the other measures as well.
Full English Alphabet
The methods used above can be extended to the entire 26 letters of the English alphabet. First lets compare the full ISA and USPA schemes with the average of 1000 random samples take from the 3-5 phoneme word pool in the same way we did for the hexadecimal case.
| Scheme | avg-phs | qual0 | qual1 | qual2 |
|---|---|---|---|---|
| ISA | 4.96 | 20.07 | 4.05 | 0.82 |
| USPA | 3.81 | 14.82 | 3.89 | 1.02 |
| rand-35 | 4.02 | 14.68 | 3.65 | 0.91 |
Table 22 Comparison of full ISA, USPA and average random sample from 3-5 phoneme words
The ISA scheme results are better here than the hexadecimal case for qual0 and qual1 against both USPA and the random samples. However for qual2 it falls below both. This reflects the significantly longer words used in ISA, averaging 4.96 phonemes compared with USPA’s 3.81 and 4.02 for the random samples.
Strangely, ISA has a number of words with the same ending sound. It has six words ending in AH, five in OW and three in ER and IY:
- AH: alpha, delta, india, lima, papa, sierra
- OW: bravo, echo, kilo, romeo, tango
- ER: november, oscar, victor (noting ER is quite close to AH)
- IY: charlie, whiskey, yankee
It is not clear whether this was by design or a coincidence, but it reduces its quality results as defined above. In comparison, USPA has five words ending in ER with all the remaining only one or two words:
- ER: baker, peter, roger, sugar, victor
The full “histogram” of finals sounds (ordered high to low) for each is:
- ISA: 6 5 3 3 2 2 1 1 1 1 1
- USPA: 5 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1
Constructed Alternatives
The same local maximum approach used for hexadecimal words above can be applied to the entire alphabet (A-Z). It produces a wider variety of possible solutions. Most have a mixture of “good” and “not-so-good” words based the categories above. One of the main issues is whether to include personal names (e.g. John, Kate, Howard, etc.). The upside is that names provide a richer set of phoneme combinations and increase the available word pool. The down side is that names are not standard english (i.e. not generally found in dictionaries) and some are more familiar than others to the general population. I’ve chosen to include them in this case.
Table 23 below shows two examples of local maximums for each of our three quality measures (labelled -a and -b). All words are again drawn from the 3-5 phoneme word pool.
| Scheme | avg-phs | qual0 | qual1 | qual2 | Words |
|---|---|---|---|---|---|
| ISA | 4.96 | 20.07 | 4.05 | 0.82 | alpha, bravo, charlie, delta, echo, foxtrot, golf, hotel, india, juliet, kilo, lima, mike, november, oscar, papa, quebec, romeo, sierra, tango, uniform, victor, whiskey, x-ray, yankee, zulu |
| USPA | 3.81 | 14.82 | 3.89 | 1.02 | able, baker, charlie, dog, easy, fox, george, how, item, jig, king, love, mike, nan, oboe, peter, queen, roger, sugar, tare, uncle, victor, william, x-ray, yoke, zebra |
| Full35-λ0-a | 4.81 | 24.68 | 5.13 | 1.07 | avenue, brother, charter, dial, ethics, future, ground, highway, input, joseph, kitchen, lottery, module, nylon, orange, piano, query, ratio, strong, tuesday, unique, value, willow, x-ray, young, zebra |
| Full35-λ0-b | 4.81 | 24.38 | 5.07 | 1.05 | alpine, blink, chester, direct, energy, future, grammar, hood, invoice, joel, kevin, locate, mature, nylon, orange, pottery, query, ratio, strong, teenage, uncle, venue, willow, x-ray, yard, zebra |
| Full35-λ1-a | 4.23 | 22.72 | 5.37 | 1.27 | address, book, choice, diana, eagle, flower, glory, heather, inch, july, katie, leo, marsh, nylon, ozone, pottery, queen, rainbow, spa, troops, unique, virtue, walter, x-ray, yoga, zebra |
| Full35-λ1-b | 4.12 | 21.81 | 5.30 | 1.29 | alpine, binary, choice, draw, eric, flyer, gourmet, hull, ink, johnny, kitchen, launch, marco, neon, over, poster, query, ratio, ski, tooth, unique, virtue, wage, x-ray, yellow, zebra |
| Full35-λ2-a | 3.19 | 15.70 | 4.92 | 1.54 | alloy, bull, chess, draw, easy, fog, garage, ham, ink, joke, keep, leo, more, nail, oboe, patch, quite, ridge, spa, town, under, view, wire, x-ray, young, zoom |
| Full35-λ2-b | 3.27 | 15.88 | 4.86 | 1.49 | alloy, beach, check, door, easy, file, grow, house, ink, join, kate, leo, myth, nest, old, poker, queen, roof, spa, top, under, view, wire, x-ray, young, zulu |
Table 23 Comparison of full ISA, USPA and two local maximums optimised for λ=0, 1 and 2
Clearly it is possible to find word sets that achieve better results than both ISA and USPA using the distance measures defined in this blog. In fact, the problem is choosing between the large number of good solutions available.
Appendix D lists some high scoring word sets using different criteria for candidate word pools and quality measures. I’ll leave it to the reader to choose their favourite.
Conclusion
The idea of using a quantitative measure to evaluate, and generate, spelling alphabets seems like a relatively straightforward exercise. However, as this post demonstrates, there are a number of complexities that make it more challenging than expected. These include:
- Mapping letters to words and their associated phonemes
- Defining a distance (i.e. difference) measure between phonemes
- Defining a distance measure between two words (i.e. two phoneme sequences)
- Defining a distance and quality measure between two groups of words
- Determining a pool of candidate words (for generation)
- Selecting words from the candidate pool to maximise a quality measure
An attempt to systematically address each of these is included in this blog.
Perhaps the most innovative element is the use of discrete convolution to measure the phonetic distance between two words. This allows different phoneme durations to be accommodated in a natural way. How well the word differences, determined by this convolution, compare with actual human perception is an open question. However it does provide a robust quantitative comparison method.
The analysis does suggest that ISA is far from optimal based on the presented measures. Even without this analysis its strange preference for words ending with AH (6 instances) and OW (5 instances) phonemes is a sign that improvement is possible. Of course its near universal adoption makes any change all but impossible. However for informal use, readers could select any of the options in Appendix D and be confident that there is at least some science behind their choice.
APPENDICES
Appendix A
Distance Normalisation and Scaling
Given a set of m points P ⊂ ℝn and a set of weights {w1, w2, …, wn} that scale each of the n dimensions, the Euclidean distance function for any two points x, y ∈ P is:
| d(x,y) = √([w1(x1-y1)]2 + [w2(x2-y2)]2 + … + [wn(xn-yn)]2) |
The requirement is to adjust the weights (wi > 0) so that in general terms:
- The contribution of each dimension is about equal that is:
- inflate dimensions that are numerically small compared with others
- deflate dimensions that are numerically large compared with others
- don’t just make a wi very small and convert the problem from ℝn to ℝn-1
- The maximum distance between any two points is 1.0
- The average (mean) distance between points is 0.5
More formally:
| 1. Σx,y∈P w1|x1-y1| ≈ Σx,y∈P w1|x2-y2| ≈ … ≈ Σx,y∈P wn|xn-yn| |
| 2. maxx,y∈P d(x,y) = 1.0 |
| 3. Σx,y∈P d(x,y) / m2 = 0.5 |
Firstly note that the entire space can be scaled by a single factor, k, to expand or contract it. This factor can thus be used to achieve either condition 2, by scaling the maximum distance to 1.0, or, condition 3, by scaling the average to be 0.5, but not both. To achieve both we need to apply a non-linear monotonic function to the weights. Here we choose to raise them to a power r.
The first condition gives the following equation for the weights:
| Σx,y∈P w1|x1-y1| = Σx,y∈P w2|x2-y2| = … = Σx,y∈P wn|xn-yn| = 1 (say) |
| w1 Σx,y∈P|x1-y1| = w2 Σx,y∈P|x2-y2| = … = wn Σx,y∈P|xn-yn| = 1 |
| wi = 1 / Σx,y∈P|xi-yi| |
| Apply a non-linear scaling power r we get: |
| wi = (1/Σx,y∈P|xi-yi|)r |
| Apply a uniform scaling factor k gives: |
| wi = k(1/Σx,y∈P|xi-yi|)r |
| or |
| wi = k(1/Δi)r = k/Δir |
| where: |
| Δi = Σx,y∈P |xi-yi| |
Substituting this back into the original distance equation gives:
| d(x,y) = √([k(x1-y1)/Δ1r]2 + … + [k(xn-yn)/Δnr]2) |
| or |
| d(x,y) = k√([(x1-y1)/Δ1r]2 + … + [(xn-yn)/Δnr]2) |
Now for any given power r (eg. r = 1.0) it is easy (with a computer :) to determine k so that the average distance is 0.5 using:
| avg = Σx,y∈P d(x,y) / m2 = 0.5 |
| Σx,y∈P k√([(x1-y1)/Δ1r]2 + … + [(xn-yn)/Δnr]2) / m2 = 0.5 |
| kΣx,y∈P √([(x1-y1)/Δ1r]2 + … + [(xn-yn)/Δnr]2) = 0.5m2 |
| k = 0.5m2 / Σx,y∈P √([(x1-y1)/Δ1r]2 + … + [(xn-yn)/Δnr]2) |
Now, by inspection of the maximum distance, r can be adjusted to move it towards its target value of 1.0. Repeated iterations using a binary search (chop) approach allows r to be determined to any appropriate level of accuracy. Once r is determined, k is known and the final weights can be calculated.
This approach may not be the most efficient but as it only needs to be carried out once it is not that critical.
Appendix B
Mean Distance between a Point and a Line Segment
The distance between a point and a line segment can be calculated numerically or analytically. Numeric approach provides an approximation by dividing the line segments into a number of equally spaced points and taking the average of the distances from the point to the line segment sub-points. Increasing the number of sub-points improves the accuracy of the result.
The analytical solution proves to be a bit trickier than one might expect. One approach is given below although alternative solutions that are more straightforward may be possible.
Consider four points P, Q, R and S in ℝn and their corresponding vectors p, q, r and s. R and S are the start and end of a line segment. Q is a point on the line segment and P is the reference point. The Euclidean distance between P and Q, or the magnitude of p–q (written p–q) is d as shown in the diagram below.
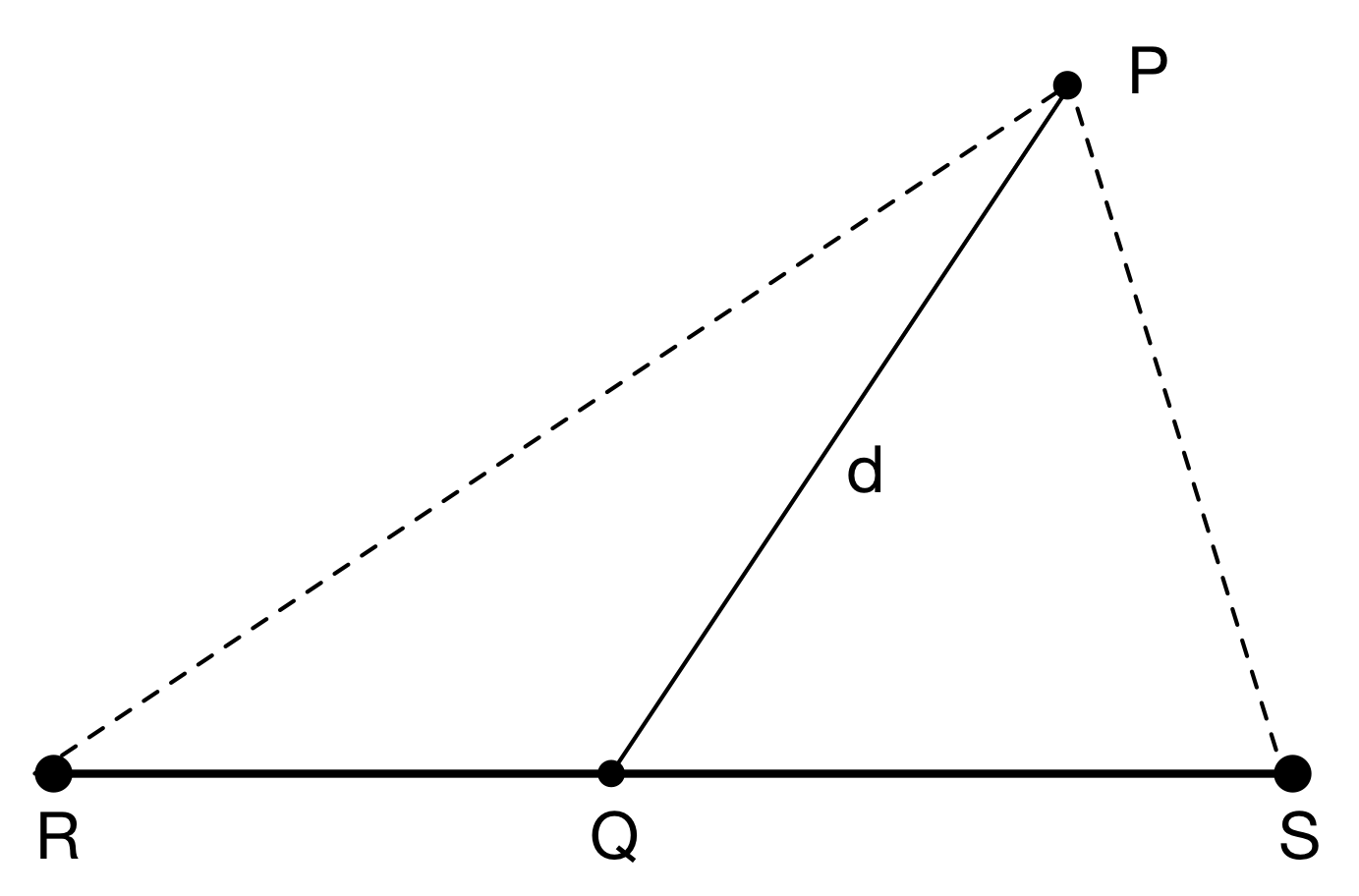
We want the mean (average) distance between P and the line segment RS.
Using the parametric definition of Q we have q = r + x(s – r) so that as x ranges from 0 to 1, q ranges from r to s.
Define the distance function, d(x), to be the magnitude of PQ (p–q) for a given x, then the mean distance is the integral of d(x) between 0 and 1. Below we use standard vector dot product algebra to expand d(x) in terms of r, s and p, and then group them in powers of x to form a quadratic equation.
| Let q = r + x(s–r) | |
| d(x) | = p–q = √(p–q).(p–q) |
| = √(p – (r+x(s–r))).(p – (r+x(s–r))) | |
| = √((p–r) – x(s–r)).((p–r) – x(s–r)) | |
| = √(s–r).(s–r)x2 – 2(s–r).(p–r)x + (p–r).(p–r) | |
| = √(ax2 + bx + c) | |
| where: | |
| a = (s–r).(s–r) | |
| b = -2(s–r).(p–r) | |
| c = (p–r).(p–r) | |
| So we have: | |
| avg-dist = ∫01 d(x) dx = ∫01 √(ax2 + bx + c) dx | |
The integral above is a bit messy but available from various mathematical applications or sites. The following is courtesy of WolframAlpha:
| ∫√(ax2 + bx + c) dx = |
| [(4ac-b2)log(2√(a)√(ax2+bx+c) + 2ax + b) + 2(2ax+b)√(a)√(ax2+bx+c)] / 8a3/2 |
The mean distance can thus be calculate by plugging in the values of a, b and c and subtracting the integral’s value at x=0 from its value at x=1.
After coding up both approaches, there was good agreement (better than 10-4) between them using 1000 sub-points for the numeric approximation.
Mean Distance between Two Line Segments
The approach taken above can be readily applied to the case of the mean distance between two line segments. Consider the following diagram.
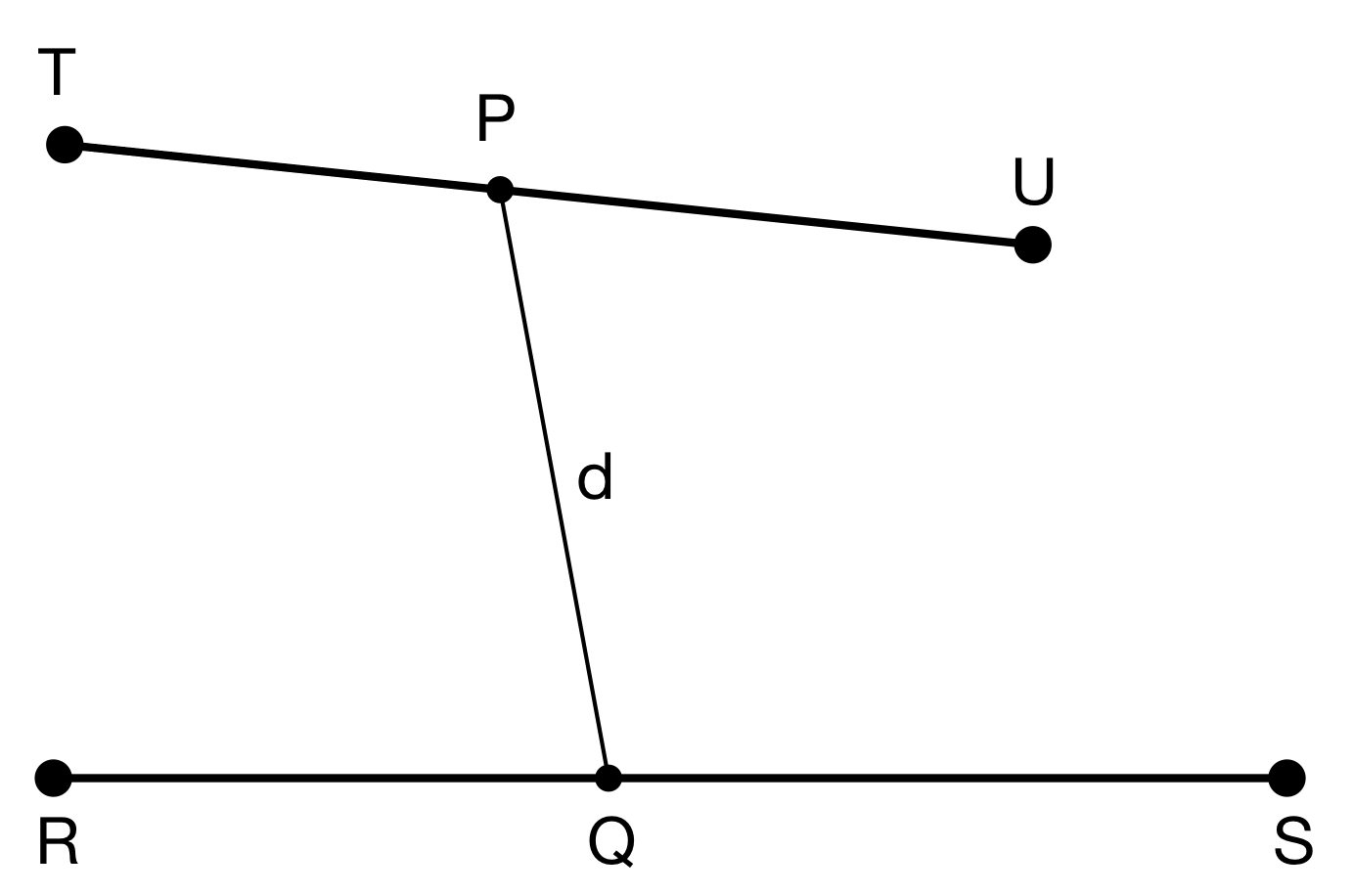
Line segments TU and RS have parametric points P and Q on them respectively. Their corresponding parametric vectors (p and q) move from T to U and R to S as x varies from 0 to 1. As above, we define the distance d between P and Q in terms of x and integrate over the range 0 to 1 to get the average distance.
More formally:
| Let p = t + x(u–t), q = r + x(s–r), giving | |
| p–q | = (t + x(u–t)) – (r + x(s–r)) |
| = x((u–t)-(s–r)) + (t–r) | |
| d(x) | = p–q = √(p–q).(p–q) |
| = √[((u–t)-(s–r)).((u–t)-(s–r))x2 + 2x((u–t)-(s–r)).(t–r) + (t–r).(t–r)] | |
| = √(ax2 + bx + c) | |
| where: | |
| a = ((u–t)-(s–r)).((u–t)-(s–r)) | |
| b = 2((u–t)-(s–r)).(t–r) | |
| c = (t–r).(t–r) | |
We can plug these values into the integral above to calculate the result.
Appendix C
Coding Discrete Convolution
Coding the convolution of two strings (or any two sequences of discrete values) can appear a bit daunting. However it is actual straightforward if you:
- reverse the second string
- lay them out in a grid, with the first string at the top and the reversed second string on the left
- calculate the value of each cell using the corresponding horizontal and vertical character (or sequence value)
- sum each of the grid diagonals to get the final convolution value
It is even easier to program if you note that the diagonal cells all have the same index sum value (i.e. the sum of the two corresponding sequence indices). This index value can be used to group the cell results into diagonals for summing.
An example will make it clear. Consider the convolution of the two strings abcd and xyz. Using the above procedure we obtain a grid as follows:

The xyz string is reversed to zyx and the δij value in the cells represent the distance between the i and j character (phoneme in our case). The small red numbers in the top right corner of the strings represents the index value of the phoneme in the string. The same numbers in the cells represent the sum of the indices of the two corresponding string phonemes. This sum can be used to programatically identify the diagonal associated with each cell. The diagonals have also been coloured for clarity. The convolution values are just the sum of the diagonals:
- convolution0 = δaz
- convolution1 = δay + δbz
- convolution2 = δax + δby + δcz
- convolution3 = δbx + δcy + δdz
- convolution4 = δcx + δdy
- convolution5 = δdx
These correspond to the string positions shown below as the two string pass each other.
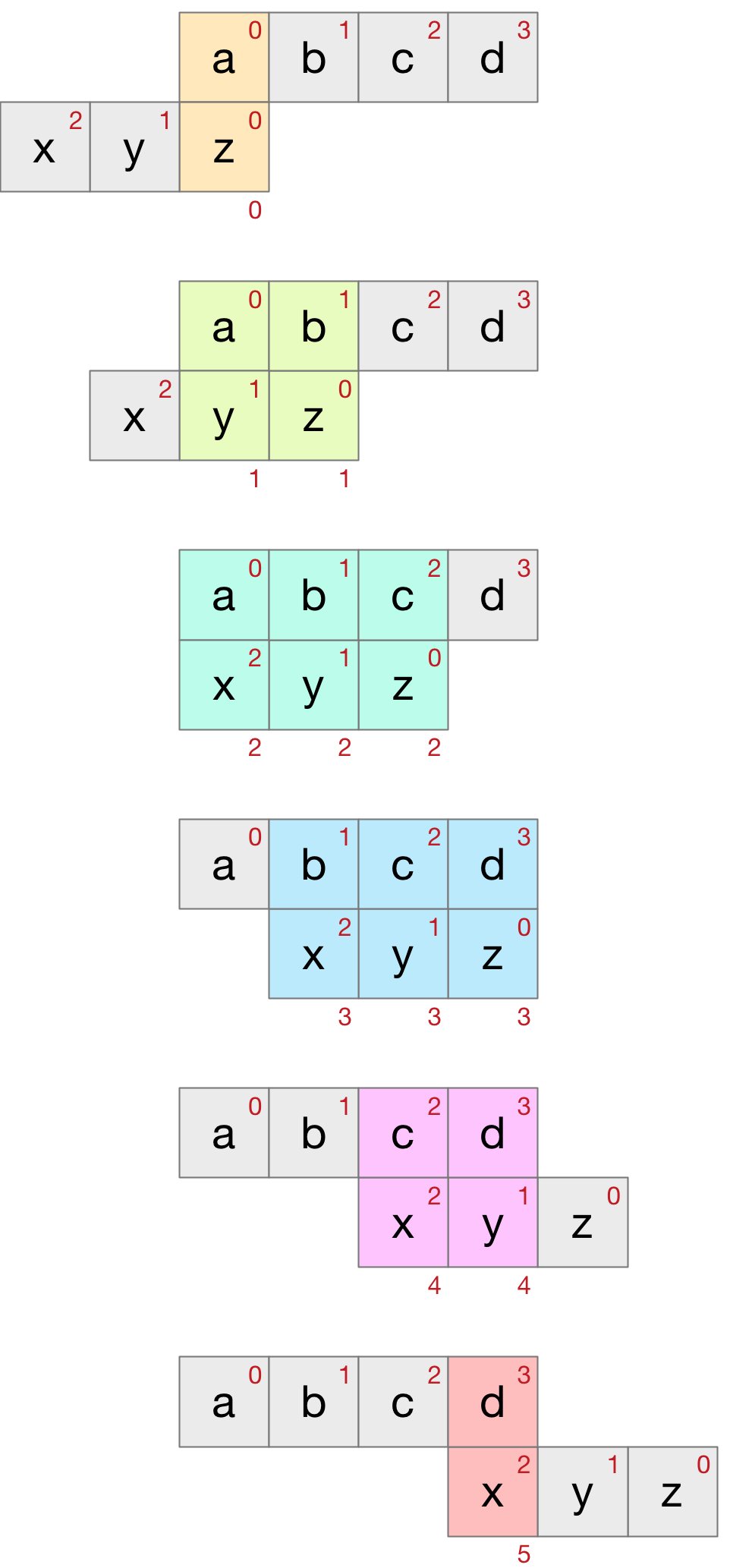
Example Clojure code might look like:
(defn convolution "Convolution of two sequences applying the function 'conv-fn' to adjacent values and summing the results." [seq1 seq2 conv-fn] (let [vec1 (vec seq1) vec2 (vec (reverse seq2)) res (reduce (fn [acc [i1 i2]] (let [cell (conv-fn (vec1 i1) (vec2 i2))] (update acc (+ i1 i2) (fnil + 0) cell))) {} (for [i1 (range (count vec1)) i2 (range (count vec2))] [i1 i2]))] (vals (sort res))))
Appendix D
Generated Example Word Sets
The following are some generated word sets using different criteria for the length of the candidate words (phoneme count) and the quality setting (λ value).
Sample 4-phoneme word sets maximising qual0 (λ=0)
The following local maximum word sets use words with exactly four phonemes. Their raw distance (qual0) is shown in brackets.
- alpha, boost, charm, diary, eric, flower, graph, hockey, icon, july, kilo, lounge, maria, neon, ozone, paper, queen, royal, score, today, under, virtue, wax, yoga, zinc (20.18)
- aqua, black, charge, diary, epic, flour, growth, hockey, image, july, kind, lewis, maria, neon, ozone, paper, queen, royal, spray, trio, under, virtue, willow, yoga, zinc (20.15)
- aqua, below, chance, diary, epic, flower, graph, hockey, image, joel, karl, launch, maria, neon, ozone, paper, queen, relay, scoop, trio, under, virtue, wealth, yoga, zinc (20.03)
- asset, broad, change, diary, eagle, flour, golf, hockey, image, july, kerry, lewis, maria, neon, ozone, paper, queen, royal, spice, trio, under, virtue, willow, yoga, zinc (19.88)
- aqua, bound, charge, deny, epic, flower, gamma, hobby, ivory, joel, kilo, lucy, mother, neon, ozone, paper, queen, relay, score, track, under, virtue, wealth, yoga, zinc (19.81)
- aqua, bother, chart, deny, eagle, flour, group, health, ivory, joel, kerry, launch, movie, neon, office, parade, queen, relay, score, trio, under, virtue, willow, yoga, zinc (19.80)
- aqua, breach, child, data, eric, flower, growth, howard, ivory, joel, kilo, launch, movie, neon, office, poker, quiz, rally, snap, today, under, virtue, wolf, yarn, zinc (19.73)
- alpha, bloom, change, depot, every, father, guru, hollow, icon, july, kerry, louise, march, neon, ozone, price, quit, royal, score, trio, under, virtue, wax, yoga, zinc (19.69)
- aqua, broad, change, diary, epic, flower, guru, hockey, image, joel, kept, luther, march, neon, ocean, paper, queen, relay, spice, trio, under, virtue, wolf, yellow, zinc (19.63)
- alpha, below, charge, drag, eric, flower, guru, highway, icon, july, kept, louise, money, nature, ozone, poem, quiz, round, spray, trio, under, visa, wales, yoga, zinc (19.58)
- alice, baker, change, dial, even, form, glad, health, ivory, july, kilo, louise, mother, neon, ozone, prior, quick, robbie, spouse, truth, under, virtue, wax, yoga, zinc (19.51)
- asset, baker, change, drag, every, flower, ghost, health, image, july, kilo, laura, maria, neon, ozone, papa, quiz, royal, speech, today, under, virtue, worthy, yarn, zinc (19.50)
- aqua, bloom, change, duty, eric, flower, graph, highway, image, july, kilo, louise, marsh, neon, often, poet, quiz, river, spray, trio, under, virtue, worthy, yoga, zinc (19.47)
- aqua, block, change, depot, eagle, flower, guru, health, ivory, july, karl, louise, mother, navy, office, past, quit, ryan, spray, truth, under, virtue, willow, yoga, zinc (19.39)
- asset, breath, change, diane, every, flower, guard, health, image, jewel, kilo, laura, movie, neighbour, ocean, poker, quote, rally, speech, today, under, virtue, wax, yeast, zinc (19.32)
- aqua, boost, charge, diary, epic, flag, guru, hello, image, july, kind, laura, marine, never, ocean, paper, quote, royal, spray, trio, under, virtue, worthy, yield, zinc (19.13)
Sample 3-phoneme word sets maximising qual0 (λ=0)
The following local maximum word sets use words with exactly three phonemes. Their raw distance (qual0) is shown in brackets.
- alloy, batch, cheap, door, easy, free, grow, height, ink, joke, ken, leo, myth, noise, oboe, pale, ross, spa, tower, view, wool, young, zoom (14.90)
- alloy, batch, choice, draw, easy, file, gate, hear, ink, judge, kim, leo, more, neck, oboe, play, ross, spa, tower, view, wool, yoke, zoom (14.74)
- alloy, batch, choice, duo, easy, fish, grey, hub, ink, jeep, ken, leo, mouth, nail, over, power, ross, spa, tall, view, wool, yoke, zoom (14.68)
- alloy, bang, cheap, door, east, full, gauge, house, ion, joke, king, leo, mug, noise, oboe, power, ruth, spa, tree, view, watch, year, zen (14.65)
- amy, batch, check, dog, era, free, grow, heath, ink, juice, keen, leo, mime, noise, oboe, power, ross, spa, tour, view, whale, young, zip (14.59)
- alloy, beach, choice, duo, easy, file, grey, hair, ion, jam, kate, leo, merge, nut, over, power, rock, spa, tall, view, wing, yoke, zoom (14.58)
- amy, beach, choice, draw, era, file, give, hall, ink, jar, kirk, leo, mouth, nan, oboe, play, race, spa, tower, view, watch, young, zoom (14.49)
- amy, blue, chief, dry, era, full, gauge, heel, ink, joan, kirk, leo, mouth, nan, oboe, power, rod, ski, touch, voice, walk, youth, zip (14.49)
- alloy, beach, choice, duo, easy, fame, grey, hood, ink, judge, kirk, long, mouth, near, oboe, poll, ruth, spa, tower, view, wife, yacht, zen (14.45)
- alloy, bush, chat, draw, east, free, gauge, hull, issue, joke, kick, leo, mayor, neil, over, paul, rock, sky, touch, voice, worth, year, zen (14.43)
- amy, bar, chief, dog, era, foam, grow, height, ink, jam, kirk, leo, match, noise, oboe, pale, rule, sky, tree, view, wire, young, zip (14.41)
- arrow, beach, chat, down, easy, few, game, hood, ink, june, kiss, leo, merge, near, over, play, rock, spa, tall, voice, wire, yoke, zen (14.38)
- alloy, batch, chase, dare, easy, firm, grey, hawk, ink, judge, keen, leo, moon, noise, oboe, power, ripe, spa, toll, view, whale, yacht, zip (14.35)
- amy, ball, choice, debt, era, flow, give, hire, ink, jar, kirk, leo, mouth, neil, oboe, page, rope, spa, tree, view, watch, young, zoom (14.30)
- alloy, bull, chase, deal, east, fare, grow, house, issue, joan, kirk, log, mayor, none, over, power, ram, spa, tree, void, watch, youth, zip (14.29)
- annie, beth, chase, duo, echo, few, goal, hood, ink, jar, keen, layer, mouth, night, over, patch, run, spa, tree, voice, walk, year, zoom (14.26)
- alloy, blue, cheap, dry, east, fog, guide, hull, ion, joke, king, leo, mouth, net, oboe, power, rush, ski, tall, voice, wage, year, zoom (14.13)
- alloy, batch, chase, dose, east, fare, grow, hire, issue, judge, keen, leo, mouth, nerve, owen, push, ross, spa, tree, void, walk, youth, zip (14.12)
- alloy, bush, chess, draw, east, few, gauge, hair, ion, june, kirk, lower, mouth, neil, oboe, play, ram, spa, tall, voice, watch, young, zip (14.10)
- alloy, blue, cheese, down, east, fell, goal, hawk, iron, jar, king, leo, mayor, none, oboe, patch, ride, spa, tree, voice, wake, youth, zip (14.08)
Sample 3-4 phoneme word sets maximising qual2 (λ=2)
The following local maximum word sets use words with three or four phonemes. Their qual2 (λ=2) is shown in brackets.
- alloy, beth, chip, draw, easy, free, girl, hire, ink, join, keen, leo, mouth, near, oboe, page, quote, run, sky, talk, under, view, wood, yacht, zoom (1.56)
- alloy, bell, choice, draw, easy, few, goal, hawk, ink, jack, kind, leo, mouth, neighbor, oboe, play, queen, rich, spa, teeth, under, virtue, wire, yacht, zoom (1.56)
- alloy, beth, chase, draw, easy, file, goal, hawk, ink, job, keep, leo, match, noise, oboe, play, quote, rear, spa, tower, under, view, wood, young, zoom (1.56)
- alloy, beef, chain, draw, easy, free, good, hire, ink, joke, kept, leo, mouth, nature, oboe, paul, quote, rock, sky, touch, under, view, worm, year, zoom (1.56)
- alloy, batch, choice, doug, easy, fall, grow, height, ink, jeep, kim, leo, mail, never, oboe, play, queen, ross, spa, town, under, view, wool, yoke, zoom (1.56)
- alloy, bench, cheat, draw, easy, feature, girl, house, ink, join, kilo, leo, myth, north, oboe, play, quick, rock, spa, tower, under, view, wage, young, zoom (1.55)
- alloy, blue, chair, doug, easy, feature, grey, hall, ion, joke, kim, leo, merge, nail, oboe, power, queen, rack, spa, tooth, under, voice, wood, yacht, zinc (1.55)
- amy, beth, choice, depot, era, full, grey, home, ink, july, keen, leo, more, none, oboe, power, quote, rack, spa, tooth, under, view, wage, yacht, zip (1.55)
- alloy, bath, choice, down, east, free, goal, hawk, icon, jake, keen, leo, moon, nature, oboe, push, quote, ross, spa, today, under, view, wire, young, zip (1.55)
- alloy, bull, choice, dog, easy, fiber, grow, hire, ink, jack, karl, leo, myth, noon, oboe, play, queen, rope, spa, town, under, view, wage, young, zen (1.54)
- alloy, beth, chat, draw, easy, free, gauge, hall, ink, joke, kerry, leo, mayor, near, oboe, peak, quiz, rock, sky, touch, under, voice, wine, yard, zoom (1.53)
- alloy, box, cheap, dash, east, file, grey, home, issue, jar, ken, leo, myth, nature, old, power, quote, roof, spa, tour, under, voice, wall, young, zinc (1.53)
- alloy, bull, chase, draw, easy, feature, grey, hawk, ink, job, keen, leo, match, noise, oboe, pair, quick, roof, spa, tower, under, view, won, yard, zip (1.52)
- alloy, ball, cheap, draw, east, few, gary, hood, iron, june, kind, leo, major, none, oboe, pitch, quick, rock, ski, tower, under, voice, worth, yoke, zinc (1.52)
- apt, book, chief, draw, easy, fall, guru, house, ivory, jack, ken, leo, mail, noise, old, play, queen, ridge, spa, touch, under, view, wire, yacht, zinc (1.52)
- alloy, bull, choose, dome, east, feature, grow, hear, issue, jake, kerry, leo, more, noise, oboe, play, queen, rug, spa, tower, under, van, watch, youth, zip (1.52)
- alloy, bull, choice, duo, east, free, gale, hawk, issue, jack, ken, logo, merge, north, owen, power, quote, ross, spa, teach, under, visa, wife, young, zip (1.51)
- alloy, bull, choose, duo, east, fairy, guard, hat, icon, join, keep, log, mouth, nature, oboe, poker, quote, rich, spa, tray, under, view, wire, young, zinc (1.50)
- amy, blue, chain, dock, east, fall, grey, hub, isaac, july, kick, leo, memo, neil, old, patch, quote, rare, spa, tiger, under, voice, wire, youth, zinc (1.50)
- act, bull, chat, door, emma, foam, grow, house, issue, judge, ken, leo, meat, noise, owen, play, quick, rock, spa, taylor, under, vary, wire, youth, zinc (1.49)
Sample 4-5 phoneme word sets maximising qual1.5 (λ=1.5)
The following local maximum word sets use words with four or five phonemes. Their qual1.5 (λ=1.5) is shown in brackets.
- alpha, bloom, child, dark, every, flour, graph, hockey, icon, july, kevin, launch, mother, neon, oscar, paper, quit, royal, score, trio, unique, virtue, willow, x-ray, yoga, zinc (2.50)
- amber, block, child, dual, eden, fridge, growth, holly, indoor, july, kilo, launch, marco, nylon, ozone, piano, query, ratio, spouse, taxi, unique, virtue, weather, x-ray, yoga, zinc (2.48)
- alex, bound, charge, diary, enter, flower, glass, hockey, image, july, kilo, leon, maria, nursery, ozone, prove, quiz, radar, score, tango, unique, virtue, wealth, x-ray, yoga, zinc (2.48)
- anchor, bother, cherry, diary, ethics, flower, gourmet, horse, image, july, karma, lounge, marine, nylon, ozone, poem, quit, ratio, school, track, unique, virtue, willow, x-ray, yoga, zebra (2.46)
- aqua, below, change, dairy, every, flower, grill, host, image, july, kitchen, louise, mother, neon, office, proper, quote, royal, speech, tank, under, virtue, width, x-ray, yarn, zebra (2.46)
- alpha, baby, change, dial, eric, flour, group, hammer, icon, july, kilo, louise, maria, north, ozone, poster, quiz, research, stock, tango, unique, virtue, want, x-ray, yoga, zinc (2.45)
- alpha, birthday, change, derek, emily, flower, ghost, highway, image, july, kilo, large, marine, nylon, ozone, patio, quiz, royal, spot, truth, unique, virtue, water, x-ray, yield, zinc (2.45)
- amateur, block, change, dual, epic, fully, growth, howard, ivory, jackie, kitchen, lucia, morris, neon, ozone, post, queen, recall, spice, trio, under, virtue, willow, x-ray, yard, zinc (2.45)
- alex, bother, chapter, daisy, every, flag, growth, heater, invoice, july, karma, louise, most, neon, often, powder, quit, royal, score, trio, unique, virtue, wild, x-ray, yellow, zinc (2.45)
- alex, beneath, charlie, decade, every, flower, greg, hockey, icon, july, kind, louise, major, neon, ozone, proper, query, royal, scoop, trio, under, virtue, warm, x-ray, yellow, zinc (2.44)
- alex, bound, charge, daily, eagle, father, group, hockey, ivory, july, kitchen, logo, matthew, neon, office, pressure, quiz, royal, stock, trio, under, viking, warm, x-ray, yellow, zinc (2.44)
- alpine, blake, charter, dual, every, forge, growth, howard, india, july, kitchen, lobby, month, nylon, office, prior, query, railway, scott, tank, uncle, virtue, willow, x-ray, yoga, zebra (2.43)
- aqua, brush, change, donor, eric, flyer, ground, howard, ivory, joel, kitchen, louise, manage, north, oscar, papa, query, ratio, spoke, today, unique, virtue, willow, x-ray, yeast, zinc (2.41)
- alice, bunch, chart, dating, emily, flower, growth, hockey, input, july, kilo, lewis, module, neon, order, parade, queen, rank, score, trio, unique, value, weather, x-ray, yoga, zebra (2.41)
- aqua, block, chance, daughter, enzyme, flyer, growth, howard, image, jewel, karl, larry, marine, nylon, oscar, piano, quit, railway, spouse, trio, unique, virtue, willow, x-ray, yeast, zinc (2.41)
- april, brad, change, daily, every, flower, gather, hockey, item, july, karl, laura, mold, neon, ozone, pillow, quote, royal, speech, tango, under, virtue, wealth, x-ray, yeast, zinc (2.41)
- andy, box, channel, dual, even, flyer, graph, horn, icon, july, kilo, lounge, major, notice, oscar, parade, quick, rubber, speech, tango, unique, virtue, worthy, x-ray, yield, zinc (2.41)
- alpha, body, charge, dual, emily, folder, guitar, highway, image, joint, kilo, luther, maria, nursery, ozone, piano, quiz, ratio, speech, trout, unique, virtue, warm, x-ray, yeast, zinc (2.41)
- alex, block, change, decor, enzyme, flyer, grill, hobby, image, jewel, karma, leon, module, nursery, oscar, parade, quote, rover, speech, tango, unique, viking, width, x-ray, yellow, zebra (2.40)
- after, broad, charge, delay, eric, future, gather, hockey, icon, jamie, kitchen, louise, month, neon, oval, parade, quiz, rainbow, solo, trio, unique, virtue, wolf, x-ray, yeast, zinc (2.38)