Tic-Tac-Toe Analysis using Clojure (Part 2)
Previously
In the first part of this blog we analysed the size and shape of the Tic-Tac-Toe (TTT), or Noughts and Crosses, game tree. We managed to prune it down from over 500,000 nodes to a few hundred by accounting for duplicated and symmetrical positions, and by considering forced moves.
While this revealed a few interesting features of TTT, such as the existence of forked positions and the three drawn patterns, it didn’t really answer key questions like:
- Can either player force a win?
- What is the best move in a given position?
In this blog we look at player strategy, TTT opening theory and position evaluation.
Basic Strategy
In general play, TTT presents each player with a number of alternative moves. While it is often clear near the end of the game that a position is a win, loss or draw, it is generally much harder towards the beginning to assess where a particular move will lead. It is a bit like following a jungle trail only to encounter a fork in the path. Without a signpost, or some other indication, it is impossible to know which path to take – one might lead to a friendly village, the other to a lions’ lair. What we need is someone to walk the paths in the reverse direction and at each fork, signpost where it leads.
We can use this approach on the TTT game tree. As all the terminal or leaf nodes are always a known result – win, loss or draw – we can work backwards and “signpost” the internal nodes.
The main differences between TTT and the jungle analogy is that in TTT:
- the players take turns in deciding which path to follow (by selecting their move)
- there are typically multiple paths (moves) at each fork
- the players have different destinations in mind: the X-player wants to go to X-wins, while the O-player wants to go to O-wins, however both would prefer a draw to a loss
To put it another way, the X-player wants to take paths that maximise the X-player’s outcome, while the O-player wants to take paths that minimise the X-player’s outcome. By assigning a numeric value, or score, to each position, from the X-players perspective (higher is better), we can restate the above as:
- X-player always chooses a move (path) with the highest score
- O-player always chooses a move (path) with the lowest score
This is known as a min-max tree and it is used extensively in game analysis. Note we are going to use a very basic non-optimised implementation here.
For our purposes, the positions will be scored as follows:
Result Score
--------------
X-win +1
Draw 0
O-win -1
Some of the same part 1 helper functions will be used in this blog. These are repeated below for convenience. The first generates all available moves. The second tests if a position is a win for the specified player.
(defn gen-moves "Return a list of all valid moves on the specified board or nil" [board] (filter #(= :e (board %)) (range 9))) (defn win-board? "Determine if a board is a win for a given player." [board player] (let [win-seqs (list [0 1 2] [3 4 5] [6 7 8] ; Horizontal [0 3 6] [1 4 7] [2 5 8] ; Vertical [0 4 8] [2 4 6]) ; Diagonal win (fn [win-seq] (every? #(= player (board %)) win-seq))] (some win win-seqs)))
The tree walking code is shown below. It is similar to that used in part 1 but in this case simply returns the score from each node. For terminal nodes this is +1, 0, or -1 depending on the X-player’s result: win, draw or loss.
For internal nodes, it returns either the maximum score of all the available moves, when those moves would be made by the X-player, or the minimum score of all the available moves, when those moves would be made by the O-player. It does this by selecting either the min or max function, depending on the next player, and applying it to the resulting scores returned by all the moves for that player.
(defn ttt-walk-scores "Recursively walk the TTT game tree returning the score for each node using min-max analysis." [board last-player next-player] (if (win-board? board last-player) (case last-player :x +1 :o -1) (let [moves (gen-moves board) minmax (case next-player :x max :o min)] (if (empty? moves) 0 (apply minmax (for [m moves] (ttt-walk-scores (assoc board m next-player) next-player last-player)))))))
This function can test any position to determine the outcome assuming each player makes the “best” move at each opportunity. The best move for the X-player is the one with the highest score, while the best move for the O-player is the one with the lowest score. If the function returns +1, it means the X-player can force a win, if it returns -1, it mean the O-player can force a win, if it returns 0 then neither player can force a win and the position can only be drawn.
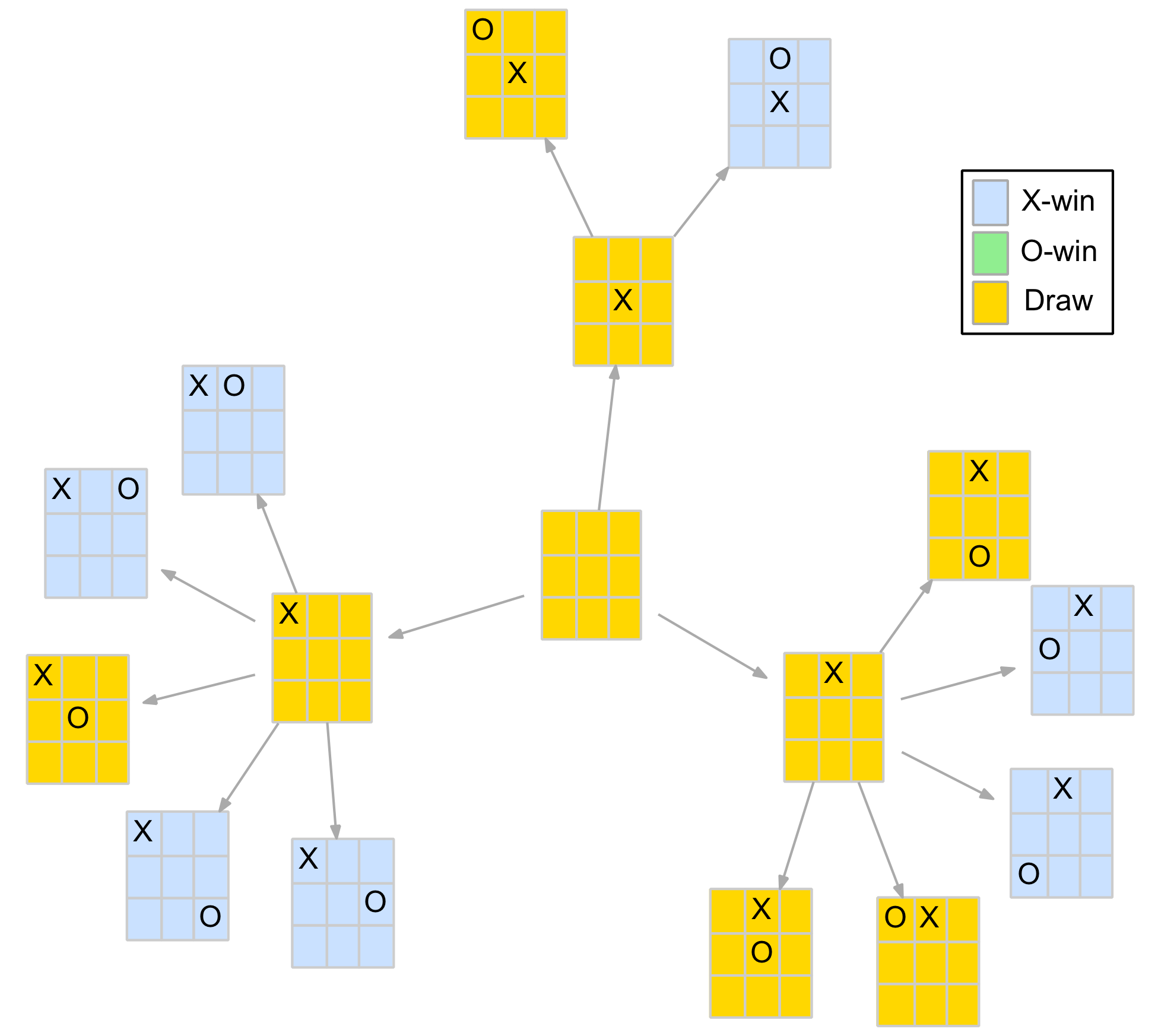
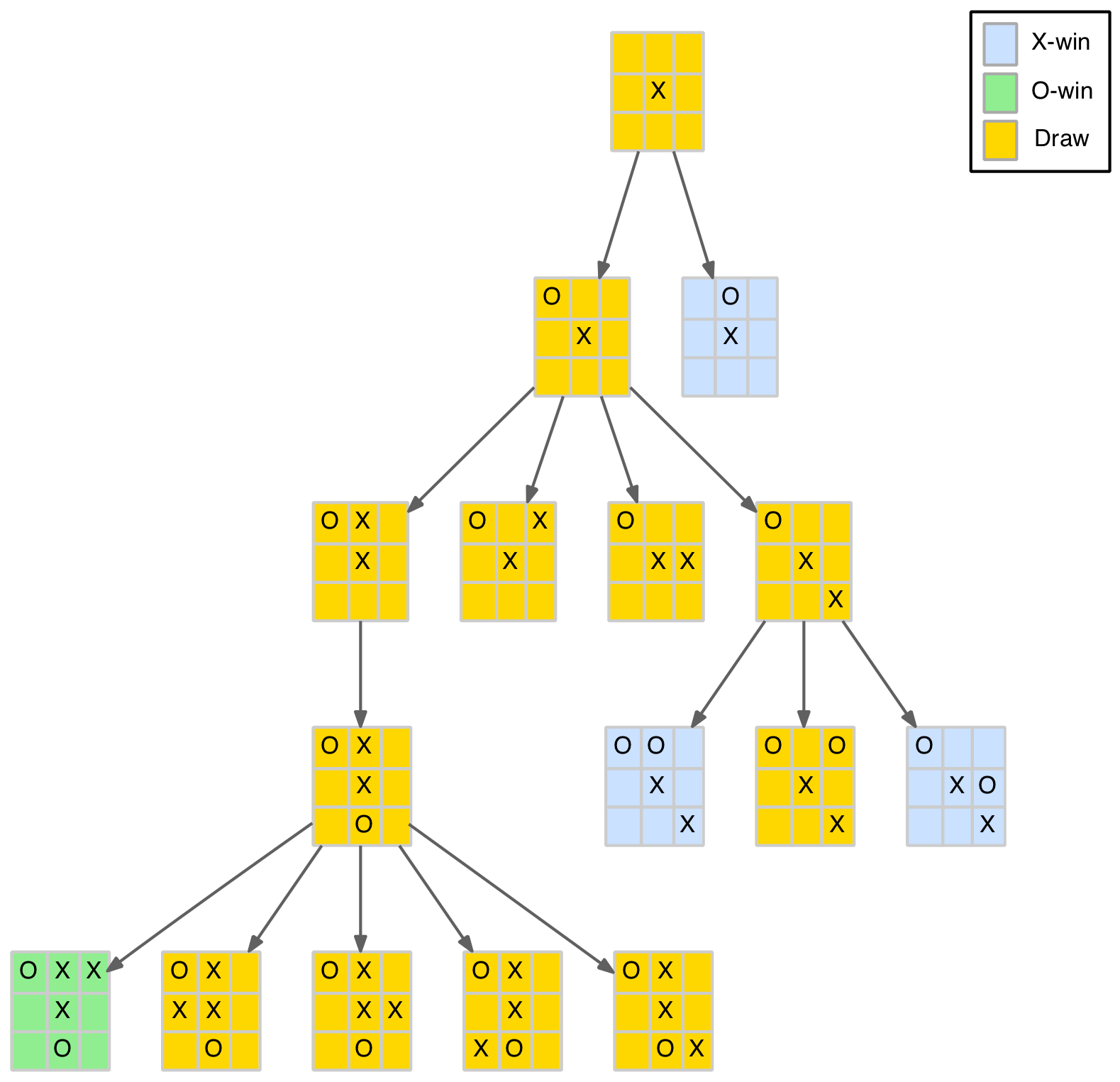
Applying the function to the positions arising from the first two opening moves (excluding symmetries) reveals some interesting results. The diagram below is the same as that used in part 1 only the nodes have been coloured to show the value returned by the function as follows:
+1 - Blue (X-player win)
0 - Gold (Draw)
-1 - Green (O-player win)
Results for the first two distinct moves
What is this diagram telling us? Well, firstly, it answers the first question at the start of this blog – can either player force a win? The fact that the initial blank board returns a draw indicates that if each player plays their best moves from the start of the game, it is always a draw. This will not surprise anyone who has played TTT, after a while it becomes evident that every game ends in a draw when played by experienced players.
It is further illustrated by the fact that all three of the X-player’s opening moves – corner, edge and centre – are also draws, which must be the case, otherwise there would be an opening move that forces a win and the blank board wouldn’t be a draw.
Secondly, it highlights the importance of the O-player’s responses to the opening moves. Of the 12 possible replies, 7 (58%) result in wins for the X-player (ie. losses for the O-player). Indeed, for the opening corner move, only one of the five possible (distinct) responses results in a draw, the other four are all losses for the O-player.
These moves represent the early opening theory of TTT. Just as chess and go have well recognised and analysed opening moves so does TTT, albeit in a much more limited way. So for the first O-player move the theory would be something like:
- On an opening corner move you MUST play in the centre
- On an opening centre move you MUST play in the corner
- On an opening edge move you have some options but the centre is safe
These could be summarised for the O-player’s first move as: always play in the centre if available, otherwise play in a corner. Later we will see that for the edge move, the O-player has a better option than the centre, although the outcome is still a draw.
While the min-max function can determine the result for any position, it is silent on how to win or draw that position. For example, it doesn’t give any direct guidance as to how the X-player should proceed to win the seven winning positions in the above diagram, should the O-player stray down one of those paths. However, by applying it to each node in the tree, it is possible to score (or colour in our case) that node. This illuminates the path, or paths, to the final goal.
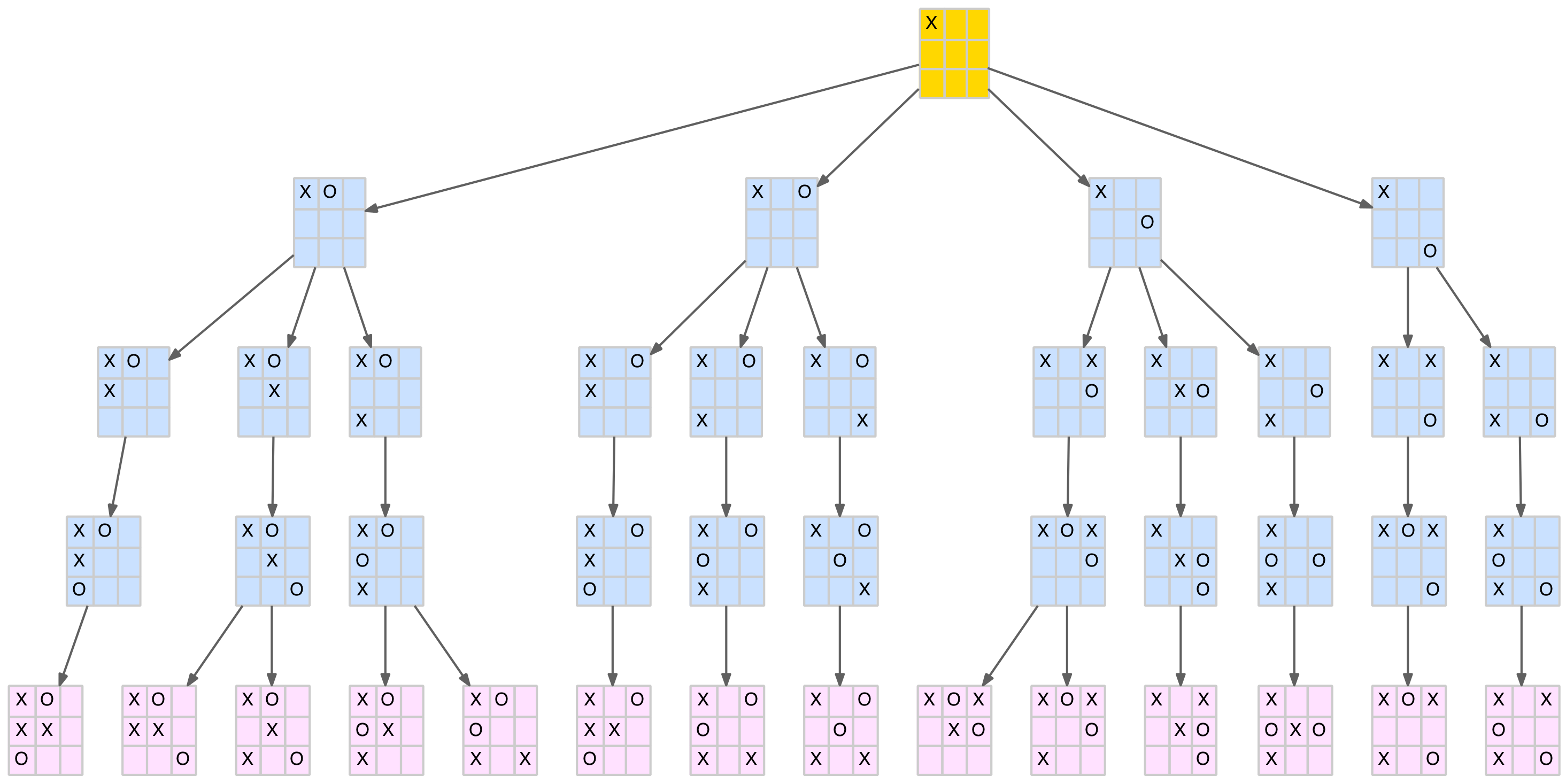
The reader has probably already realised that the X-player’s winning positions arise because they can be turned into a forked position (a position where there are two two-in-a-row threats of which the opponent can only block one). In many cases, there are several ways to create a fork from these positions. The following diagrams show all the ways to force a forked position (shown in pink), and therefore a win, from the seven losing O-player responses.
Forced wins from the corner opening move
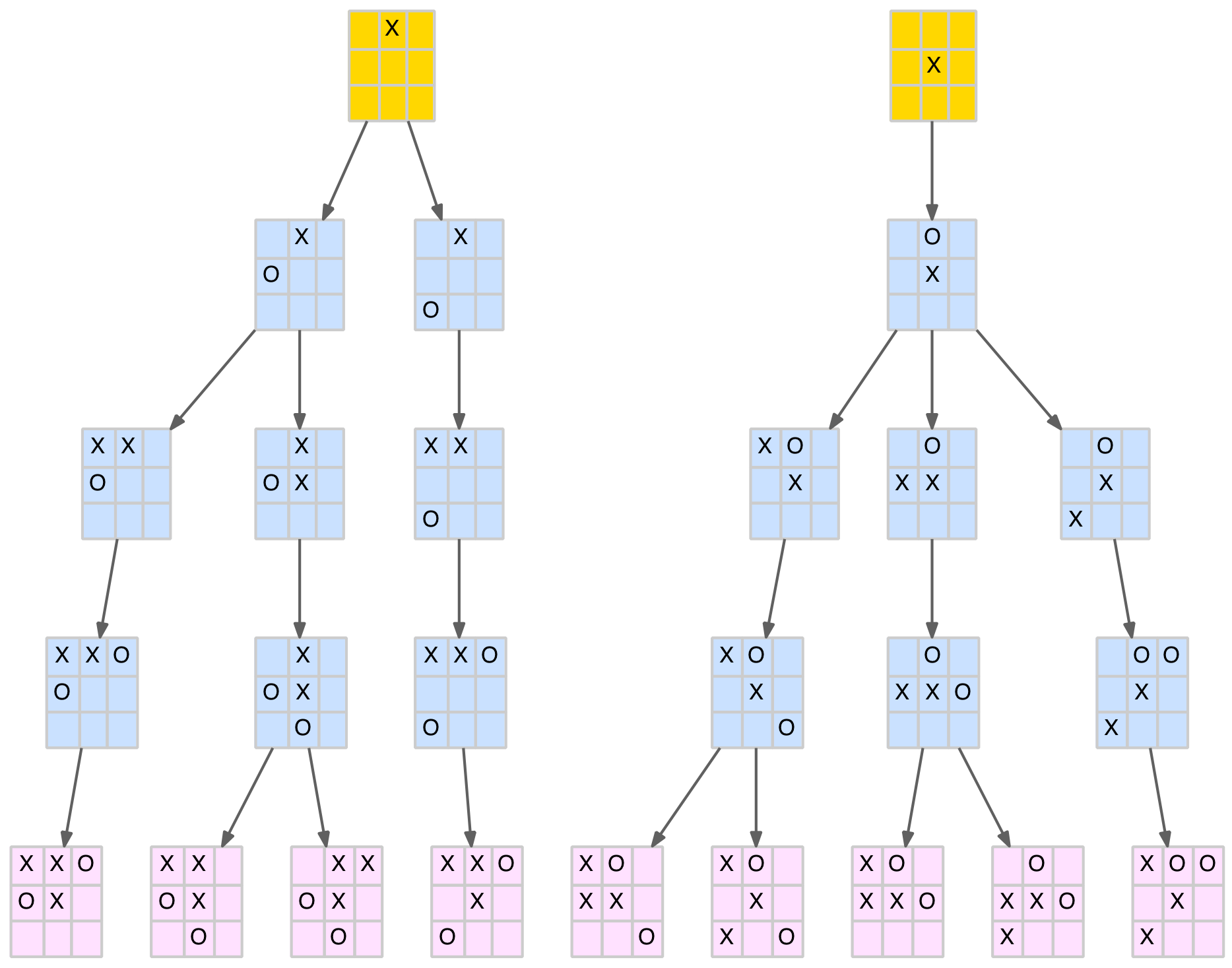
Forced wins from the edge and centre opening moves
It is not really necessary to memorise these as with a little practice you can look ahead and visualise the forked position(s). This guides you to the correct play. It is more important to know when a position is winning (or losing) so you can search for the correct play to reach the forked position. It is worth noting that all the paths to a forked position in these cases starts with the X-player making a forcing move (ie. one that requires the O-player to block immediately).
So X-player’s thinking goes like this:
- Oh, good, O-player has fallen into an opening trap, and is toast
- Let me consider all the forcing moves I have and the O-player’s (forced) response
- From these positions which ones have a move to create a fork
Of course, if you are playing a novice, and you have egotistical tendencies, it is worth varying the opening move orientation and type of fork as much as possible, to reduce the chance that the pattern will be recognised and avoided in the future. After all, toast is toast.
Extended Opening Theory
So far we have only considered the first two opening moves. These are important because it is not obvious that the game can be won, or lost, so early on. But what about later moves? We can extend the opening theory by considered a game tree where we stop (ie. deem a node to be terminal) on the following conditions:
- The node is a win (or will lead to a win) for the X-player or the O-player (as determined by the min-max function)
- The node is a drawn position AND there are no forked positions later in the tree (as determined by a similar function not shown here)
These conditions mean the tree only extends as far as either an inevitable win/loss or a pedestrian draw (ie. no fork positions – traps – are possible) position. This tree represents the essential essence of the game as all the “traps” are exposed and the path to a draw is clear. However, it does not extend into the details of how to win the won positions or how to draw the drawn ones. The former is left to the reader (with some examples above), the latter is just a matter of blocking any two-in-a-row threats (safe in the knowledge that there are no forks lurking). This makes the tree fairly compact and concise. For the remainder of the blog, this tree will be referred to as the reduced game tree.
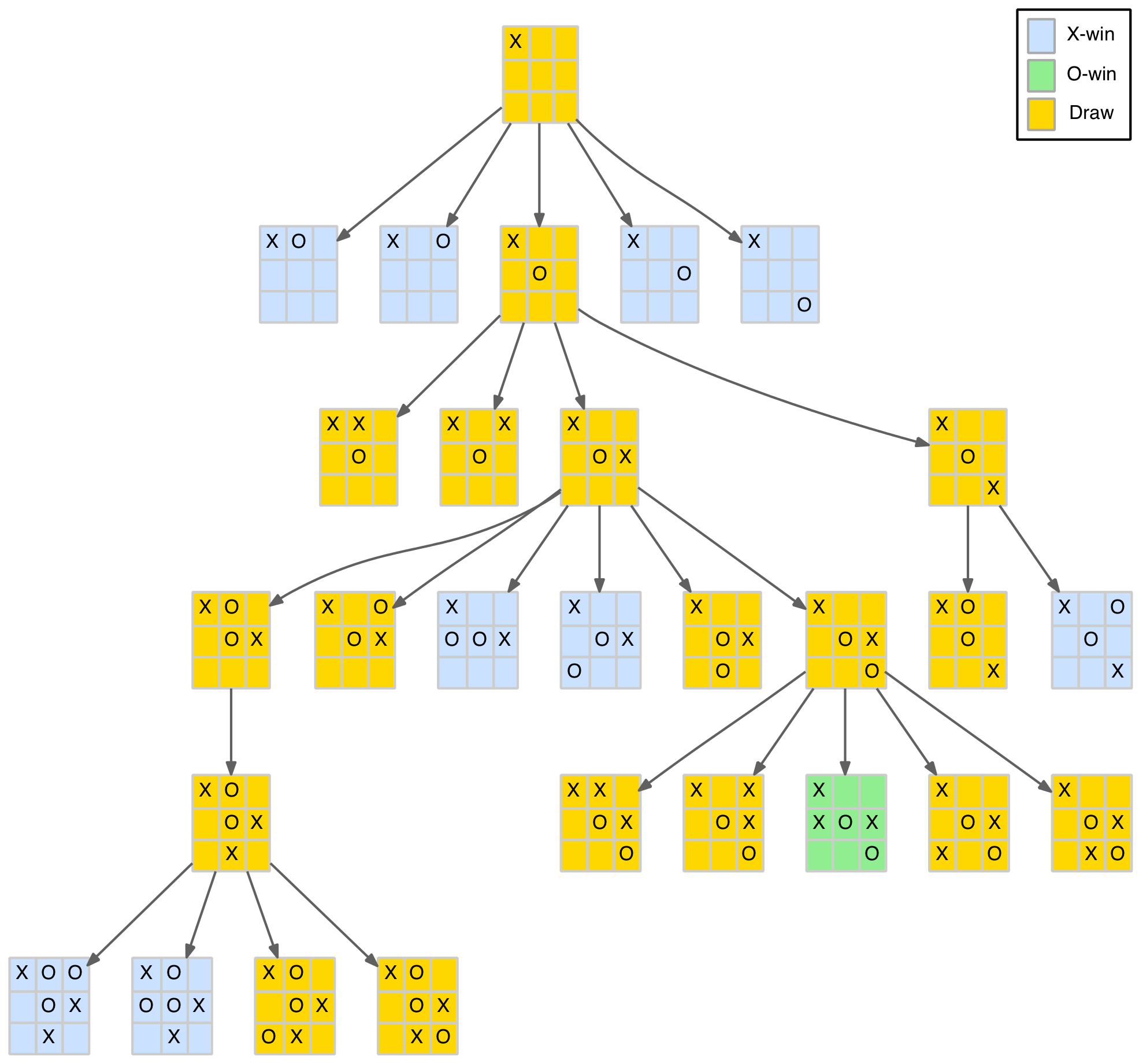
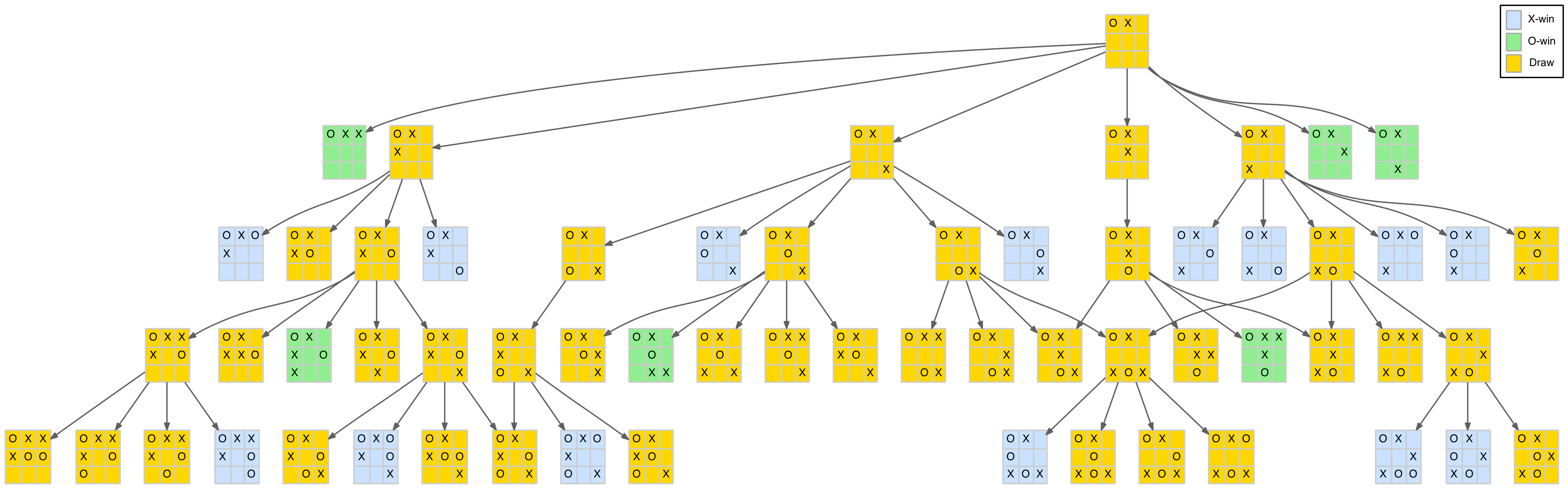
The diagram below shows the opening corner move branch of the reduced game tree.
Reduced game tree for the corner opening move
What can we glean from this branch of the tree? Well, the second level is as described earlier with four of the five O-player responses resulting in X-player wins. After the O-player’s (forced) centre play there are four (distinct) X-player responses. The first two are pedestrian draws (provided each player just blocks correctly). The last two moves are a bit more interesting as they can lead to forked positions.
The last play (opposite corner) sets a small but fairly obvious trap. The O-player must now play an edge, not a corner move. After that it is a standard draw.
The third move (opposite edge) is the most interesting. It sets up a couple of immediate losing options for the O-player, as well as two more at level 6 (far left branch). It also shows, for the first time, that the O-player can set a trap as well (path to the green node) by playing in the bottom-right corner.
In summary, after the corner opening and (forced) centre reply position, the X-player has the opposite corner for a simple and safe trap, or the more edgy (excuse the pun) opposite edge that has a few more traps including one for the O-player. In this line, the O-player needs to navigate around the blue positions above to achieve a draw.
Now let’s look at the opening centre move of the reduced game tree.
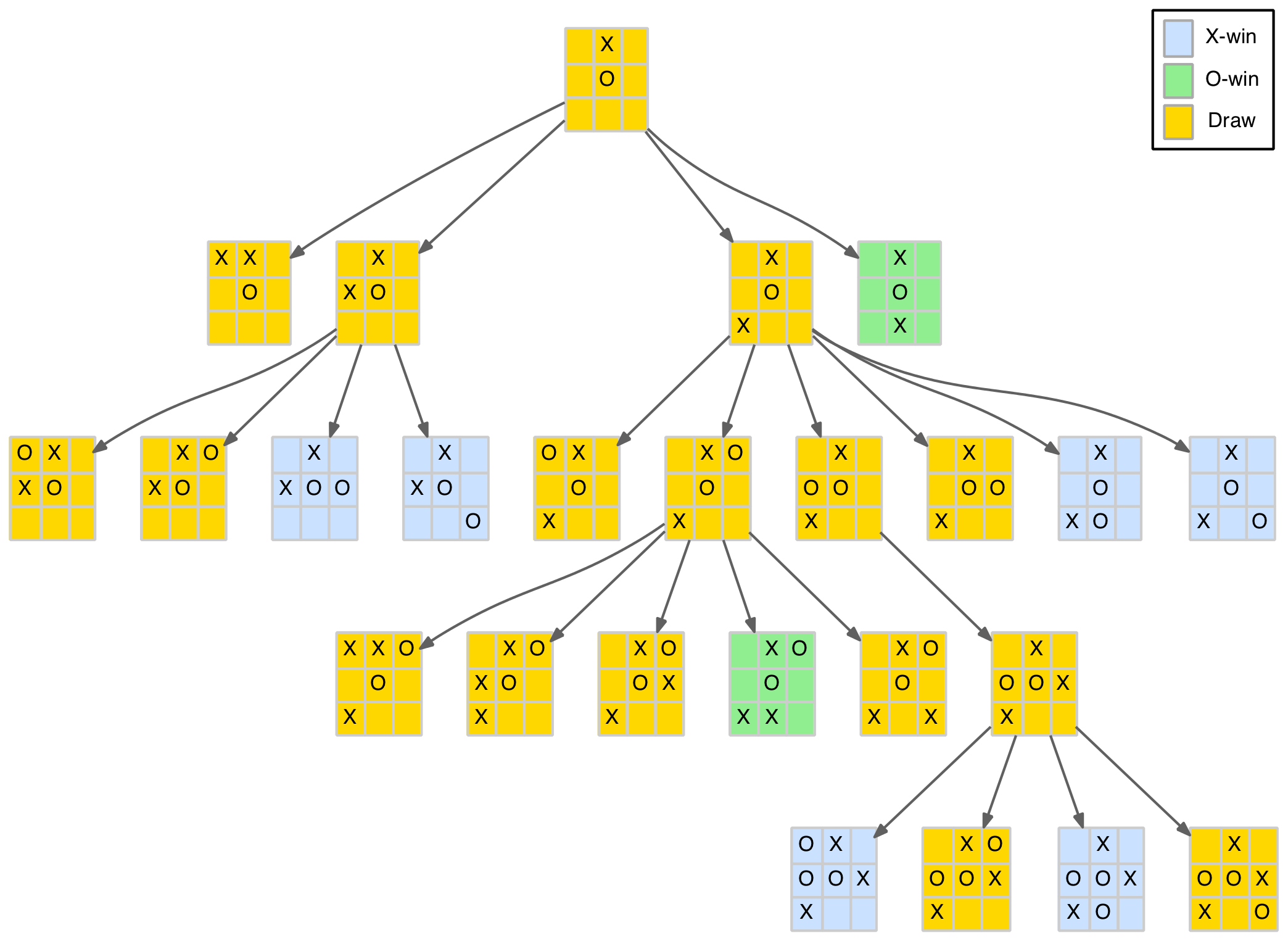
Reduced game tree for the centre opening move
As mentioned above, the O-player must play in a corner to avoid defeat. After that the X-player has four (distinct) plays. All but the last – opposite corner – lead to standard draws, or even a possible loss in the case of the bottom left path. But after the opposite corner play, the O-player must play in the corner again to force a draw. So the somewhat benign looking opposite corner is actually a little tricky.
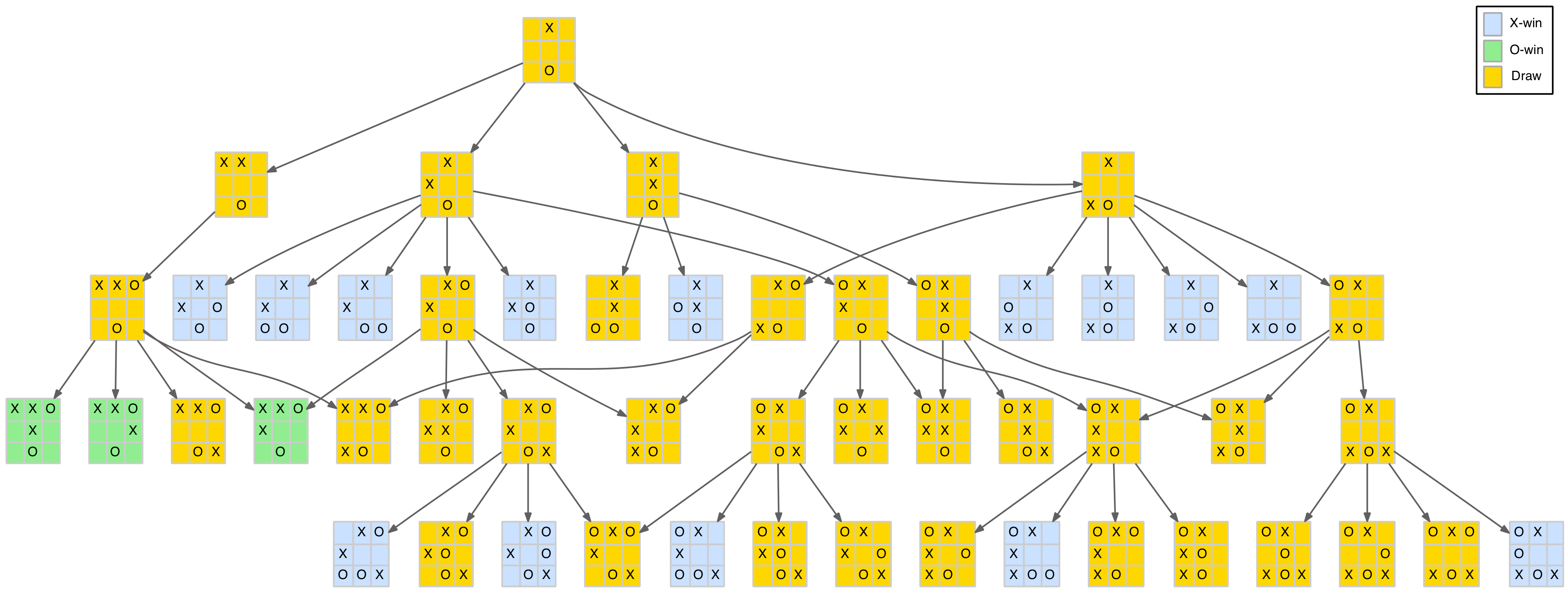
The next, and last, of the X-player’s opening moves is the edge play. You might expect this to yield a similarly compact reduced tree as the other two. However, it actually produces a bit of a monster with 95 nodes. To fit it in the blog it has been broken down into the three, level 2 responses, that aren’t direct wins for the X-player.
Reduced game trees for the edge opening move (broken into three parts)
Once the tree gets this large it is more difficult to analyse by hand (or eye). Can we develop a scoring system and apply the min-max approach to the reduced tree in the same way we did for the entire tree above?
Best TTT Moves
The second question at the start of this blog was: what is the best move in a given position? This question assumes we have a definition of “best”.
If we work with the reduced tree where we stop and mark a node as terminal (or leaf), if it leads to an inevitable win, loss or standard draw (assuming sensible blocking aways occurs), we can use the same approach as above. Scoring from the X-player’s perspective, we can mark a win as +1, a loss as -1, and a draw as 0.
For internal nodes, we can assume the score is an average of its child nodes. In effect, this assumes that a player will make a random move where there is no clear alternative. The result is an assessment of the value of each position which can be used as a proxy for “best”. The complete scored reduced tree is too large to display directly in the blog but two links to pdf versions follow:
- Scored Reduced Game Tree – excludes duplicate nodes but has more cross links
- Scored Reduced Game Tree – removes all cross links but has some nodes duplicated
Each node’s score is shown on the link to that node. All the symmetric links are included (red lines) so the average score is a true representation of all the available moves.
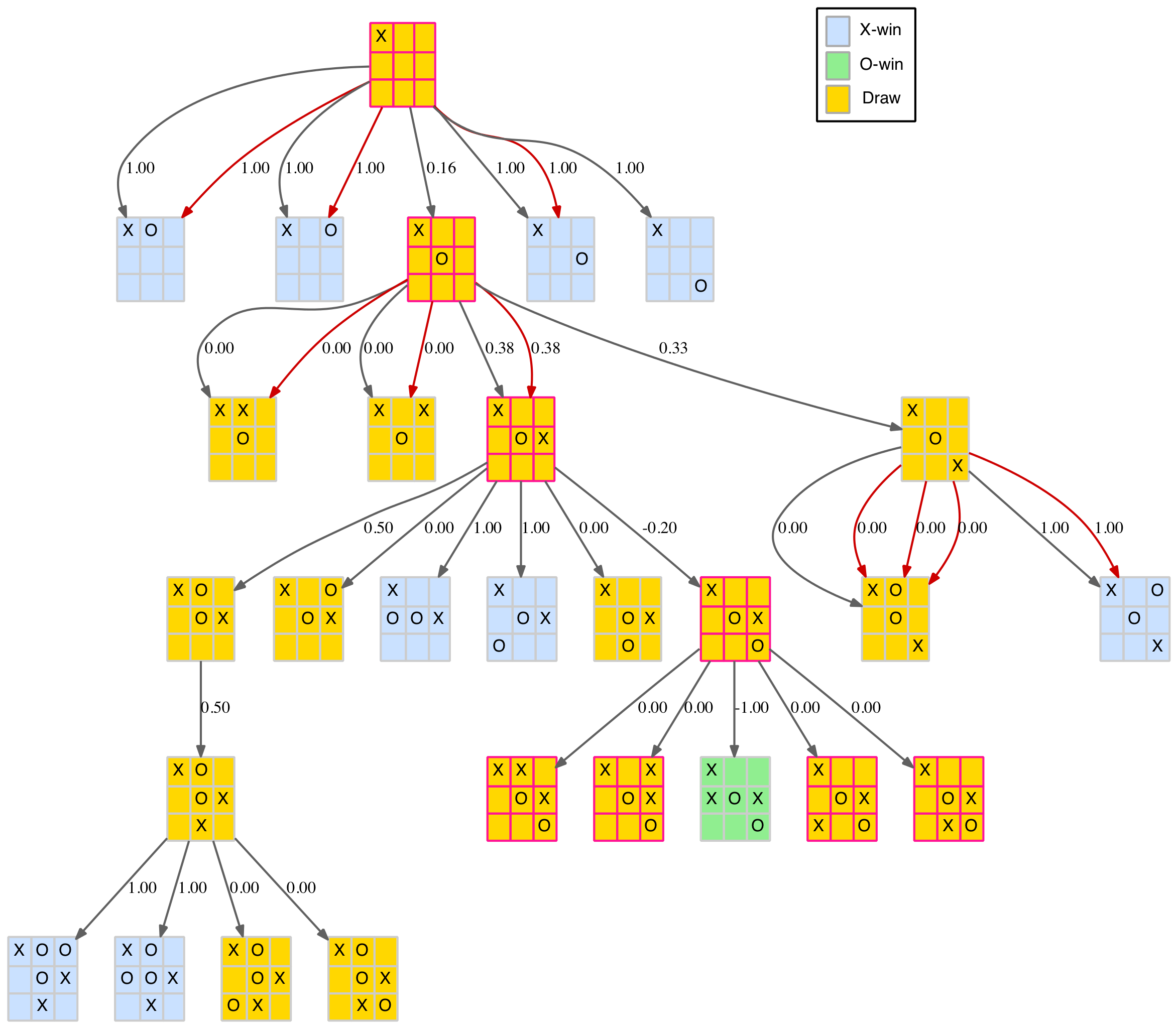
The corner-play branch of this tree, which has the highest scoring (0.89) first move, is shown below.
Corner opening reduced tree with scores
By applying the min-max rule we can plot a path for the “best” move for each player. For the X-player’s move we choose the move with the highest score, for the O-player’s move we choose the lowest. The path is highlighted in the above diagram. This notionally represents the best TTT game possible, or at least the first four moves. On the fifth move the X-player has a choice of four moves which, of course, all end in a standard draw (with correct blocking play).
The scored tree above assumes that symmetric moves are included and are equally likely to be played in any given position. An alternative approach is to exclude symmetric moves. In effect this means that the players still play randomly, where there is no clear alternative, but only consider distinct moves, ignoring those that are simply symmetries of a previous move. This does not change the tree structure but does affect the scoring slightly as show in the revised reduced tree pdf:
- Scored Reduced Game Tree – excluding symmetries (also with duplicates)
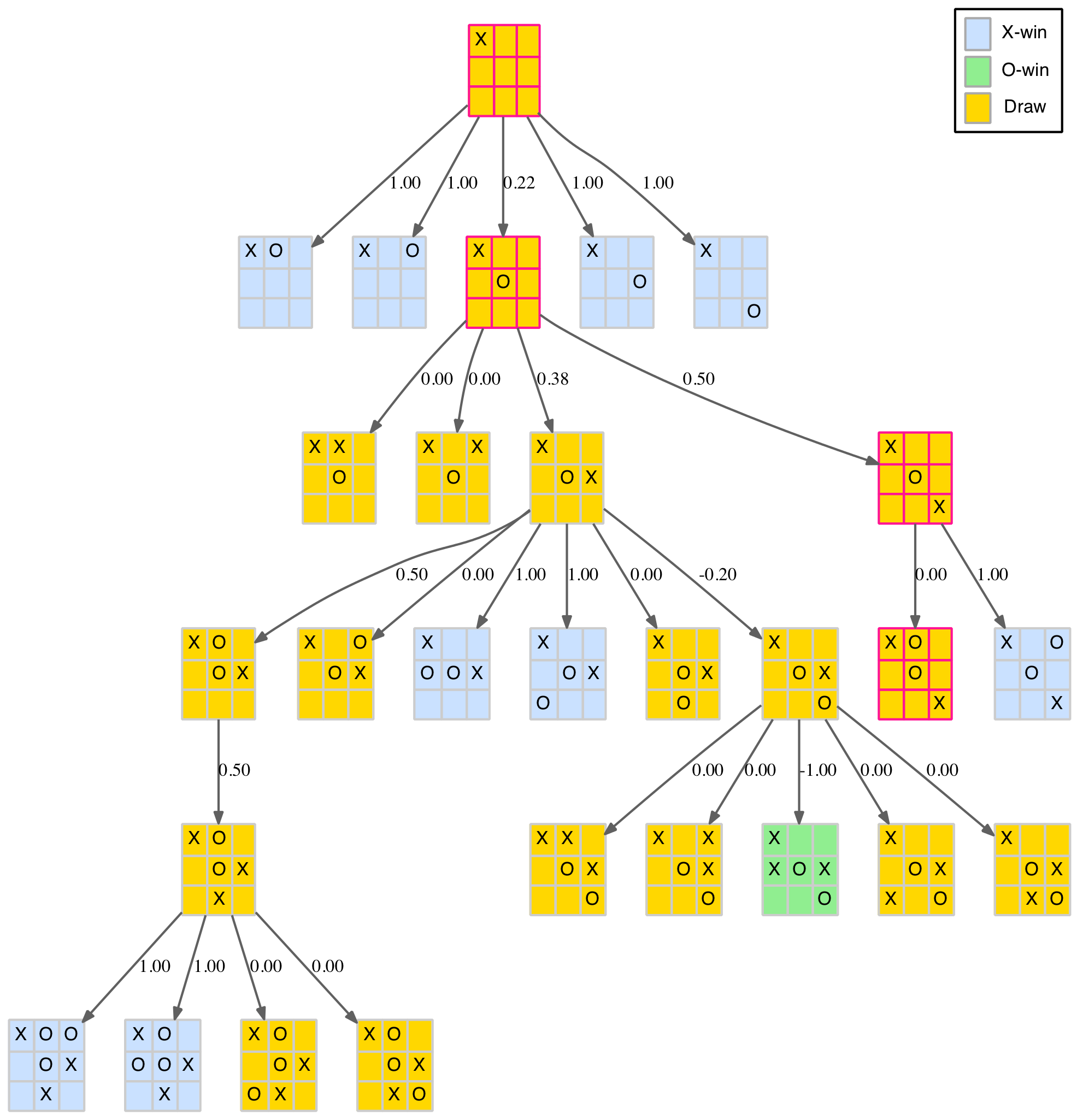
In particular, the “best” game now takes a different path as shown in the revised corner branch below.
Corner opening reduced tree with scores excluding symmetries
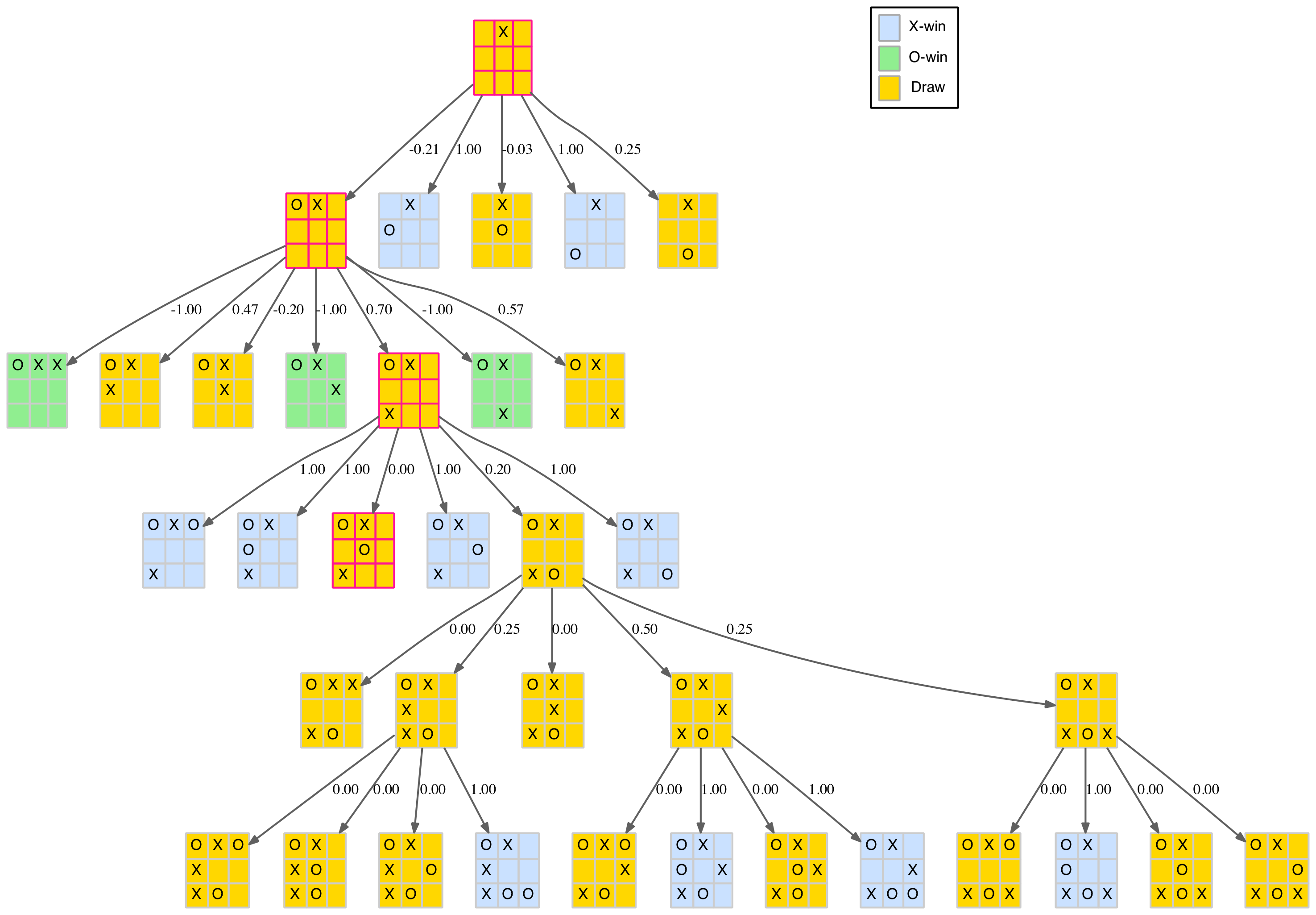
Briefly returning to the opening edge play which we skipped earlier as the tree was quite large. With the aid of the position scores, it is now easy to see that the O-player’s best response is a corner on the same edge. As shown in the partial tree below, this creates three losing options (out of seven distinct plays) for the X-player. The X-player’s best reply is the same corner on the opposite edge, which then leads to a draw once the O-player plays in the centre.
Partial edge opening move reduced tree with scores
The initial edge play is technically the weakest from the X-player’s perspective. It opens the way for many forked positions on both sides, but perhaps because of this, it is also the most interesting in many ways.
This completes the TTT strategic analysis. The links to the full reduced game trees above (especially the last two) provide a clear and concise description of the complete TTT game. In a sense they capture the essence of the game including a realistic score for each key position.
Drawn Position Patterns
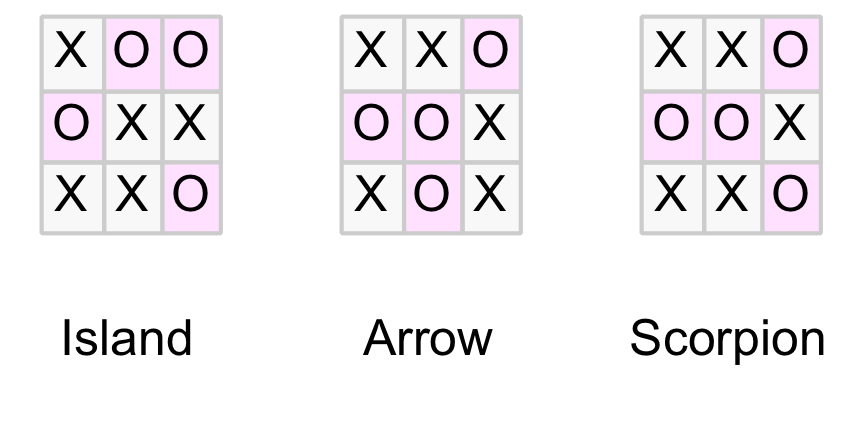
In part 1 of this blog we discovered that all drawn positions form one of the following three patterns.
Drawn Position Patterns
Clearly the X-player can always force the Island pattern by playing in the centre on the first move (as it is the only pattern with an “X” in the centre). But what about the other two? Can the X-player force the game to a particular drawn pattern?
We can modify the earlier min-max code to distinguish between different drawn patterns and assign a non-zero score to the one we are interested in testing. A helper function, to determine the draw type, and the modified min-max code is shown below.
(defn draw-pattern "Examine the specified board and return the drawn pattern type" [board] (if (= :x (board 4)) ; 'x' in the centre --> Island :island (if (= 2 (count (filter #{:o} (map board [0 2 6 8])))) :scorpion ; 'o' in two corners --> Scorpion :arrow))) ; otherwise --> Arrow
(defn ttt-walk-scores "Recursively walk the TTT game tree returning the score for each node using min-max analysis." [board last-player next-player] (if (win-board? board last-player) (case last-player :x +10 :o -10) (let [moves (gen-moves board) minmax (case next-player :x max :o min)] (if (empty? moves) (case (draw-pattern board) :island 0 :arrow +1 :scorpion 0) (apply minmax (for [m moves] (ttt-walk-scores (assoc board m next-player) next-player last-player)))))))
By setting the win and loss scores up to +10 and -10, some room is made to give a small integer score to the drawn patterns (of course we could use fractional scores but this keeps changes to a minimum). Using +1 for a specific drawn pattern (Arrow in the above case) and leaving the others as zero means the min-max function will try to select a path to a drawn position of this pattern for an X-player move and away from this pattern for an O-player move.
Using this method we can construct the table below for each pattern, for the initial position and for the first three opening moves.
Position Island Arrow Scorpion
-------------------------------------
Initial Yes Yes Yes
Corner No Yes No
Edge No No Yes
Centre Yes No No
The table shows that the X-player can, indeed, force a draw in any of the three patterns from the initial blank board. However, the first move is critical to which pattern can be forced. For example, to ensure a Scorpion draw the X-player must start with an edge move. Note in the case of the Arrow and Scorpion draws, these initial moves are a necessary but not sufficient condition. The X-player still needs to select the correct moves later in the game to guarantee the result.
Incorporating drawn position patterns into the game could be used to make it more interesting. For example, a running score over a fixed number of games could decide the winner using a scoring scheme like the following:
Result X-player O-player
-------------------------------
X-win 3 0
O-win 0 5
Island draw 0 1
Arrow draw 0 1
Scorpion draw 1 0
While this can be subverted by extending the draw analysis above (with the X-player in the box seat) it may keep the kids entertained a bit longer. There is a little bit of science in the above scoring scheme but it hasn’t been road-tested, other variations may well work better in practice.
Summary
Part 2 of the blog has focused on player strategy. Using the min-max function, we learned that:
- The game is always a draw if each player makes optimal moves
- Knowing some opening theory is important as 7 of the 12 first O-player moves result in a forced loss
Extending the opening theory to produce a reduced game tree exposes all the traps arising from forked positions. It also captures the essence of the entire game in fewer than 200 nodes. Assigning scores to this tree allows each (interesting) position to be evaluated and the ‘best’ move in a given position determined. This leads to the notion of the perfect game.
Finally, drawn positions were briefly analysed and considered for inclusion in a scoring scheme to enhance the game’s interest.