Alternative Warp Speed Scale

At the risk–hopefully not too great–of offending Star Trek enthusiasts and traditionalists, it seems that a simple update to the Warp speed definitions would allow for more realistic exploration of space without departing unduly from the original concept.

The update would use a simple base-10 log scale. Log scales are often used in science and technology with Decibel and Richter scales being common examples.

Under this revision, a Starship’s speed or velocity (v) would be defined as:

v = 10w-1c	…(1)
where:
v = velocity (speed)
w = Warp speed
c = speed of light

Equation 1 above uses w-1 (rather than just w) as the exponent to preserve Warp 1 as the speed of light (c), since 10⁰ = 1, which is in keeping with existing scales and the general understanding of Warp speeds. Warp 2 becomes 10 times the speed of light, Warp 3 is 100 times, etc.

Table 1 is a comparison with existing Warp speed factors (multiples of the speed of light):

Warp	TOS (w3)	TNG/DS9/VOY	Proposed (10w-1)
1	1	1	1
2	8	10	10
3	27	39	100
4	64	102	1000
5	125	214	10,000
6	216	392	100,000
7	343	656	1M
8	512	1024	10M
9	729	1516	100M
9.9	–	3053	794M
9.99	–	7912	977M
10	Not possible	Not possible	1000M (see below)

Table 1 Comparison of Traditional and Proposed Warp Speed Factors

Series abbreviations:

• TOS = The Original Series
• TNG = The Next Generation
• DS9 = Deep Space Nine
• VOY = Voyager

The main advantages of the proposed approach are that it:

• aligns reasonably well, and in some cases better, with time/distance in the TV/film series
• makes the galaxy more navigable in human time frames
• makes intergalactic travel plausible
• would relax the somewhat artificial and tortured Warp 10 limit, however, this can be restored in a more mathematically rigorous way (see below)

While the proposed speeds are significantly greater than the standard scales, at least for higher Warp values, they fit more comfortably with the vast distances found in our Universe. For example, using the old scale (TNG say), to travel from Earth to the centre of our galaxy, about 25,000 light years, it would take over 16 years at Warp 9 and over 3 years at Warp 9.99.

Going to another (close) galaxy is simply implausible, taking 300 or more years at Warp 9.99. Given there are hundreds of billions of galaxies out there, it seems a bit limiting to restrict exploration to such a tiny fraction of the known universe.

By contrast, Table 2 below shows a distance and travel time chart for the proposed new scale.

Warp	Local Planets	Nearby stars	Visible stars	Federation	Centre of galaxy	Cross galaxy	Nearby galaxies
	(0.0005 ly)	(50 ly)	(500 ly)	(5,000 ly)	(25,000 ly)	(100,000 ly)	(5 Million ly)
1	4.4 hr	50.0 yr	500 yr	5,000 yr	25,000 yr	100,000 yr	5,000,000 yr
2	26.3 min	5.0 yr	50.0 yr	500 yr	2,500 yr	10,000 yr	500,000 yr
3	2.6 min	6.0 mth	5.0 yr	50.0 yr	250 yr	1,000 yr	50,000 yr
4	15.8 sec	2.6 wk	6.0 mth	5.0 yr	25.0 yr	100 yr	5,000 yr
5	1.6 sec	1.8 day	2.6 wk	6.0 mth	2.5 yr	10.0 yr	500 yr
6	0.16 sec	4.4 hr	1.8 day	2.6 wk	3.0 mth	1.0 yr	50.0 yr
7	16 msec	26.3 min	4.4 hr	1.8 day	1.3 wk	1.2 mth	5.0 yr
8	1.6 msec	2.6 min	26.3 min	4.4 hr	21.9 hr	3.6 day	6.0 mth
9	0.16 msec	15.8 sec	2.6 min	26.3 min	2.2 hr	8.8 hr	2.6 wk
10	0.016 msec	1.6 sec	15.8 sec	2.6 min	13.1 min	52.6 min	1.8 day

Table 2 Distance and Travel Times for the Proposed New Warp Speeds

Remembering that a scale is just that, a scale. It doesn’t mean that starships can reach these speeds or sustain them for extended periods. Indeed, standard cruising speed may be significantly less than full speed because of engine stress and energy efficiency.

The next section builds on these ideas by placing limits on Warp speed based on various criteria.

Warp Speed Constraints

To provide limits on the speed of Warp capable ships, and to stay faithful to the idea of a universal maximum Warp speed, for example Warp 10, we can introduce some constraints. One approach is a blend of relativistic and newtonian mechanics.

First, let’s assume that:

1. The force required to move a ship though the Warp field is proportional to the square of its Warp speed, and,
2. There is an universal maximum Warp speed (μ) similar to the speed of light in standard physics

Based on these two assumptions, the force (F) required to “push” through the Warp field can be written mathematically as:

F = aw2 / √(μ2-w2)	…(2)
where:
F = force
a = constant
w = warp speed
μ = universal maximum warp speed

The numerator is the Warp squared factor from the first assumption above. The denominator is analogous to the Lorentz factor of special relativity which is usually written 1/√(c²-v²). It means the required force increases as the speed approaches the universal maximum Warp speed and becoming infinite at that maximum Warp speed. This meets the second assumption above and provides a robust mathematical underpinning of the limit.

Using the force definition from Equation 2 and the velocity from Equation 1, we can calculate the Power (P) required by a Warp engine to maintain a constant velocity using the standard relation:

• Power (P) = Force (F) by velocity (v)

This gives:

P = Fv = acw210w-1 / √(μ2-w2)	…(3)
where:
P = power
F = force
v = velocity (speed)
a = constant
c = speed of light
w = warp speed
μ = universal maximum warp speed

From Equation 3 the energy needed to travel a particular distance can be derived using the standard definitions:

• distance (d) = velocity (v) by time (t)
• Energy (E) = Power (P) by time (t)

This leads to the following energy equation:

d = vt
E = Pt = (Fv)t = F(vt) = Fd = adw2 / √(μ2-w2)	…(4)
where:
E = energy
P = power
F = force
v = velocity (speed)
t = time
d = distance
a = constant
w = warp speed
μ = universal maximum warp speed

In addition to power and energy calculations, we can derive an equation for efficient defined as the distance travelled per unit of energy consumed (similar to fuel efficiency for motor vehicles). The efficiency (eff) equation follows directly from Equation 4:

eff = d/E = √(μ2-w2) / aw2

…(5)

Setting a Universal Maximum Warp (μ)

We can choose any Warp speed as the universal maximum, but let’s stay with convention and make μ=10.

The constant a in the above equations depends on the “units” we use to measure the various quantities. For simplicity, let’s make P=1 when w=1. We can put these values into the Power equation (3) above and solve for a as follows:

1 = ac12101-1 / √(102-12)
1 = ac / √(102-12)
ac = √(102-12) = √99
a = √99 / c

Then substituting a back into Equations 3 gives:

Pμ=10 = √99w210w-1 / √(100-w2)

…(6)

Using the same approach for the Energy and Efficiency equations, namely:

• Energy = 1 per unit distance (say 1 lightyear) when w = 1
• Efficiency = 1 (100%) when w = 1

We get:

Eμ=10 = √99w2 / √(100-w2) per unit distance	…(7)
effμ=10 = √(100-w2) / √99w2	…(8)

Table 3 below shows comparative results for Power, Energy and Efficiency for various Warp speeds based on Equations 6, 7 and 8. It also includes the time it would take to travel one light year at the given Warp speed as a reference.

Warp	Power	Energy per ly	Efficiency (%)	Time to travel 1 ly
1	1	1.0	100.00	1.0 yr
2	41	4.1	24.62	1.2 mth
3	939	9.4	10.65	3.6 day
4	17,370	17.4	5.76	8.8 hr
5	287,228	28.7	3.48	52.6 min
6	4,477,443	44.8	2.23	5.3 min
7	68,269,794	68.3	1.46	31.5 sec
8	1,061,319,933	106.1	0.94	3.2 sec
9	18,489,527,619	184.9	0.54	0.32 sec

Table 3 Comparative Power, Energy and Efficiency for Various Warp Speeds (μ=10)

These results show that:

• Power requirements rapidly (exponentially) increase as Warp speeds increase
• Energy (fuel) requirements modestly increase as Warp speeds increase
• Efficiency, which is essentially the inverse of energy consumption, reduces in line with energy increases

The massive power requirements speak to the difficulty of achieving higher Warp speeds. It confirms the understanding that significant technical advances are required to go just one step up the Warp speed ladder. It also supports the idea that even a fractional increase in Warp speed comes at a significant cost in terms of additional power requirements.

While the power demands are very high at higher Warp speeds, the energy consumption (i.e. fuel use) remains relatively modest (although increasing). This means the main technical challenge in Warp drive design is to convert the available energy at a high enough rate to provide the power demands needed to achieve a given Warp speed.

The energy efficiency figures can be interpreted, in starship terms, as light years per unit of fuel, for example antimatter. So you get, say, 100 light years per kilogram of antimatter at Warp 1, but only 24.6 at Warp 2, and this drops down to just over half a light year (0.54) at Warp 9, of course you cover that half light year in a fraction of a second!

Despite the rather hypothetical situation, the overall results are consistent with what we might expect from Starship pseudo physics or, perhaps, Warp drive mechanics.

Engine Power Levels

We can further expand on these results to show how the engine power output affects Warp speeds. Lets assume full speed – the rated top speed – is achieved when the engine is producing 100% of its rated power output. Table 4 below shows the corresponding Warp speeds associated with various percentages of this power output for different rated Warp speeds (leftmost column).

Rated Warp	20%	40%	60%	80%	100%	120%	140%	160%	180%	200%
2	1.5	1.7	1.8	1.9	2.0	2.1	2.1	2.1	2.2	2.2
3	2.5	2.7	2.8	2.9	3.0	3.1	3.1	3.2	3.2	3.2
4	3.4	3.7	3.8	3.9	4.0	4.1	4.1	4.2	4.2	4.2
5	4.4	4.7	4.8	4.9	5.0	5.1	5.1	5.2	5.2	5.3
6	5.4	5.7	5.8	5.9	6.0	6.1	6.1	6.2	6.2	6.3
7	6.4	6.7	6.8	6.9	7.0	7.1	7.1	7.2	7.2	7.3
8	7.4	7.7	7.8	7.9	8.0	8.1	8.1	8.2	8.2	8.2
9	8.4	8.7	8.8	8.9	9.0	9.1	9.1	9.2	9.2	9.2

Table 4 Warp Speeds for Various Engine Power Percentages (μ=10)

Table 4 shows that running on lower power settings doesn’t significantly reduce the Warp speed compared with its rated full speed (100% power). And conversely, running the engine above its rated power (i.e. overloading it) produces only marginal gains in Warp speed.

Based on this observation, let’s assume Starfleet defines the following Warp speed/power designations:

Designation	Percentage of Rated Power	Description
Reserve Warp	10%	Energy conservation or damaged engine
Standard Warp	33%	Standard cruising speed, default if no speed specified
Express Warp	67%	Expedited speed
Full Warp	100%	Rated full speed
Flank1 Warp	133%	Flank speed (medium overload)
Maximum Warp	167%	Maximum speed (maximum overload), emergency situations

Table 5 Starfleet Designations with Associated Rated Power Percentages

1. Flank is a US nautical term used to denote speeds in excess of “full” speed.

Using these Starfleet designations, the corresponding Warp speeds, and the time to travel one lightyear (ly) at those speeds, for different Warp rated ships are shown in Table 6 below.

Rated Warp	Designation	Reserve	Standard	Express	Full	Flank	Maximum
	Power %	10%	33%	67%	100%	133%	167%
2	Warp	1.3	1.7	1.9	2.0	2.1	2.2
	Time/ly	5.4 mth	2.5 mth	1.6 mth	1.2 mth	4.3 wk	3.6 wk
3	Warp	2.3	2.6	2.9	3.0	3.1	3.2
	Time/ly	2.9 wk	1.2 wk	5.0 day	3.7 day	2.9 day	2.5 day
4	Warp	3.2	3.6	3.9	4.0	4.1	4.2
	Time/ly	2.3 day	21.1 hr	12.1 hr	8.8 hr	6.9 hr	5.8 hr
5	Warp	4.2	4.6	4.9	5.0	5.1	5.2
	Time/ly	5.8 hr	2.2 hr	1.2 hr	52.6 min	41.4 min	34.3 min
6	Warp	5.2	5.6	5.9	6.0	6.1	6.2
	Time/ly	36.3 min	13.3 min	7.4 min	5.3 min	4.1 min	3.4 min
7	Warp	6.2	6.6	6.9	7.0	7.1	7.2
	Time/ly	3.7 min	1.3 min	44.4 sec	31.5 sec	24.7 sec	20.5 sec
8	Warp	7.2	7.6	7.9	8.0	8.1	8.2
	Time/ly	21.7 sec	7.9 sec	4.4 sec	3.2 sec	2.5 sec	2.1 sec
9	Warp	8.2	8.6	8.9	9.0	9.1	9.2
	Time/ly	2.0 sec	0.75 sec	0.43 sec	0.32 sec	0.25 sec	0.21 sec

Table 6 Actual Warp Speed and Time to Travel 1 ly for Starfleet Designated Speeds (μ=10)

This means a starship that is rated as Warp 5, for instance, has a standard cruising speed of Warp 4.6 and maximum speed of Warp 5.2. However, there are two main reasons why ships cannot simply run at their maximum Warp speed:

• Energy cost (fuel)
• Engine endurance

We have already looked at energy consumption and seen that energy efficiency does reduce significantly at higher Warp speeds, but an even stronger reason to reduce Warp speed is engine endurance. This is explored in more detail in the next section.

Engine Endurance

Engine endurance is the length of time the engine can operate at a particular power output level before it requires maintenance. Typically Warp engines must be taken offline for a period to allow the maintenance to be performed.

Without maintenance, the risk of a major engine failure or even a catastrophic engine breach significantly increases.

I’m givin’ it all she’s got, Captain! If I push it any farther, the whole thing’ll blow!

– Montgomery ‘Scotty’ Scott

The higher the output power, and hence Warp speed, the shorter the operating time. Conversely, the lower the power output the longer the engine can run before requiring maintenance.

The engine endurance is a function of the ratio of actual engine power compared to the rated (100%) engine power (ρ = P / P_r). This ratio is one (1) when the actual power equals the rated power. Less than one when the actual power is lower than the rated power, such as cruising, and greater than one in overload situations.

There are various ways to formulate an endurance equation but let’s assume that Starfleet Warp drives have an endurance (ε) characterised by an inverted sigmoid function.

As a refresher, the following graphs show a “standard” sigmoid function and some progressive variations to transform it into something more suitable for use as an endurance function.

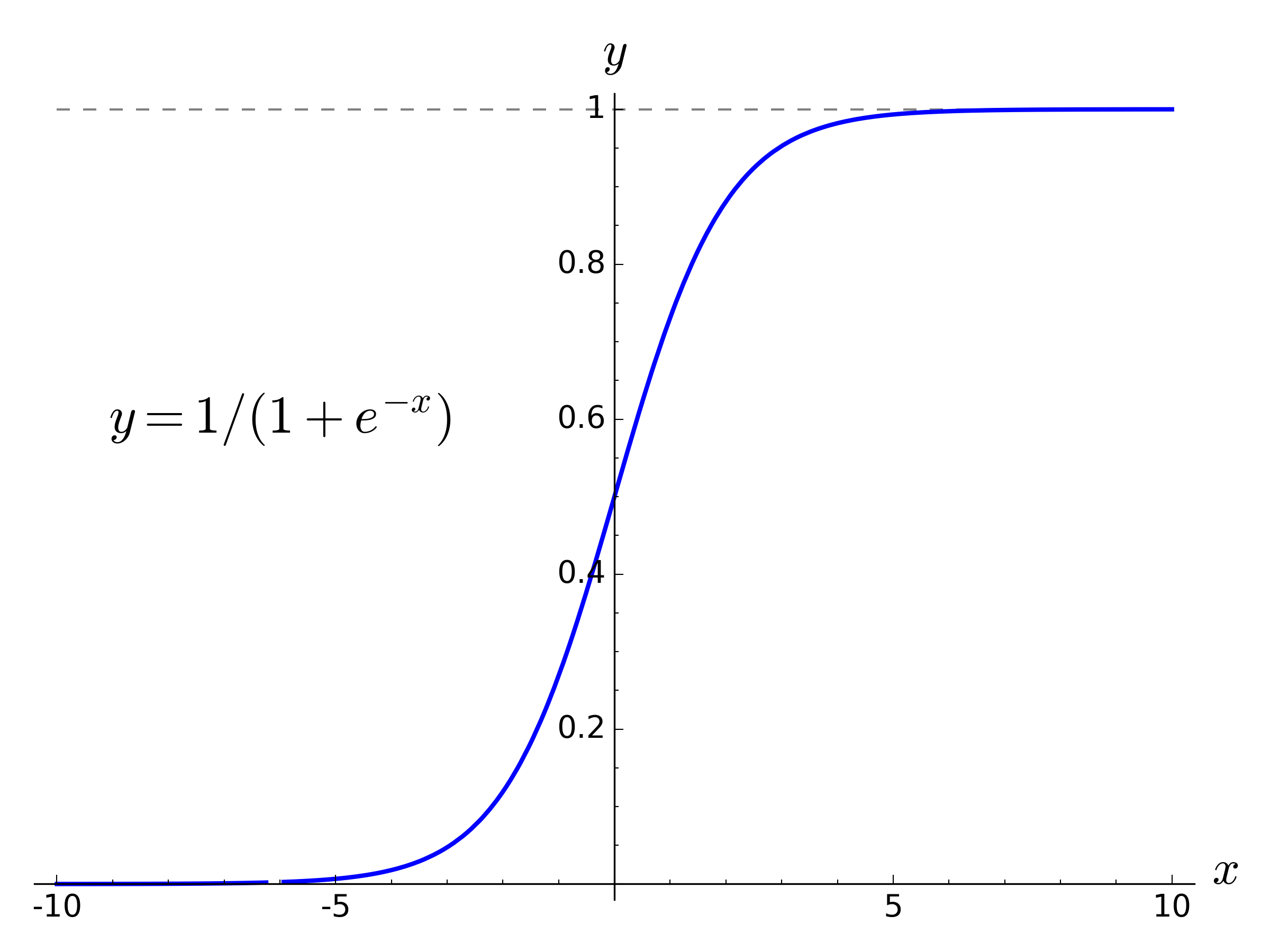
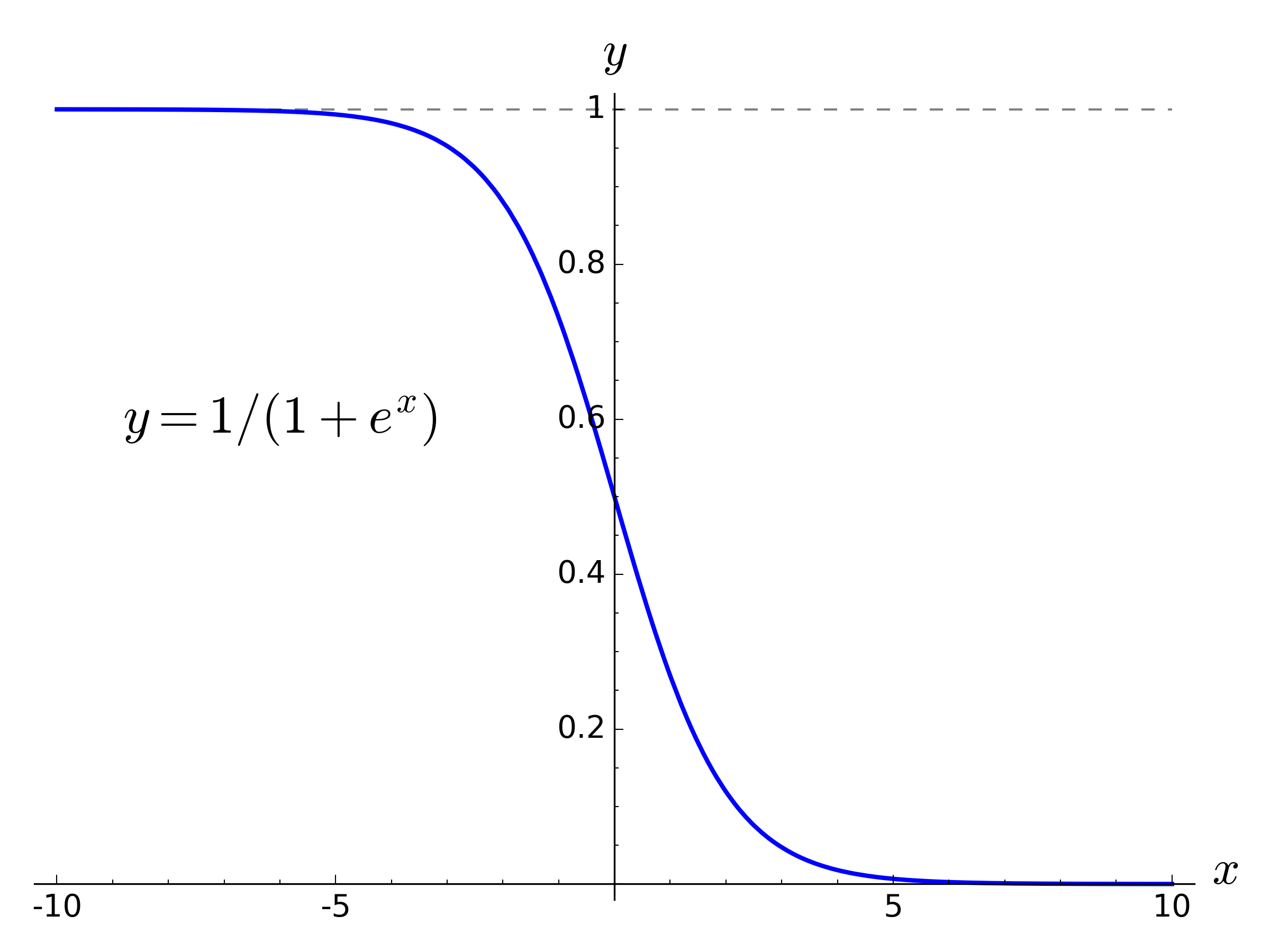
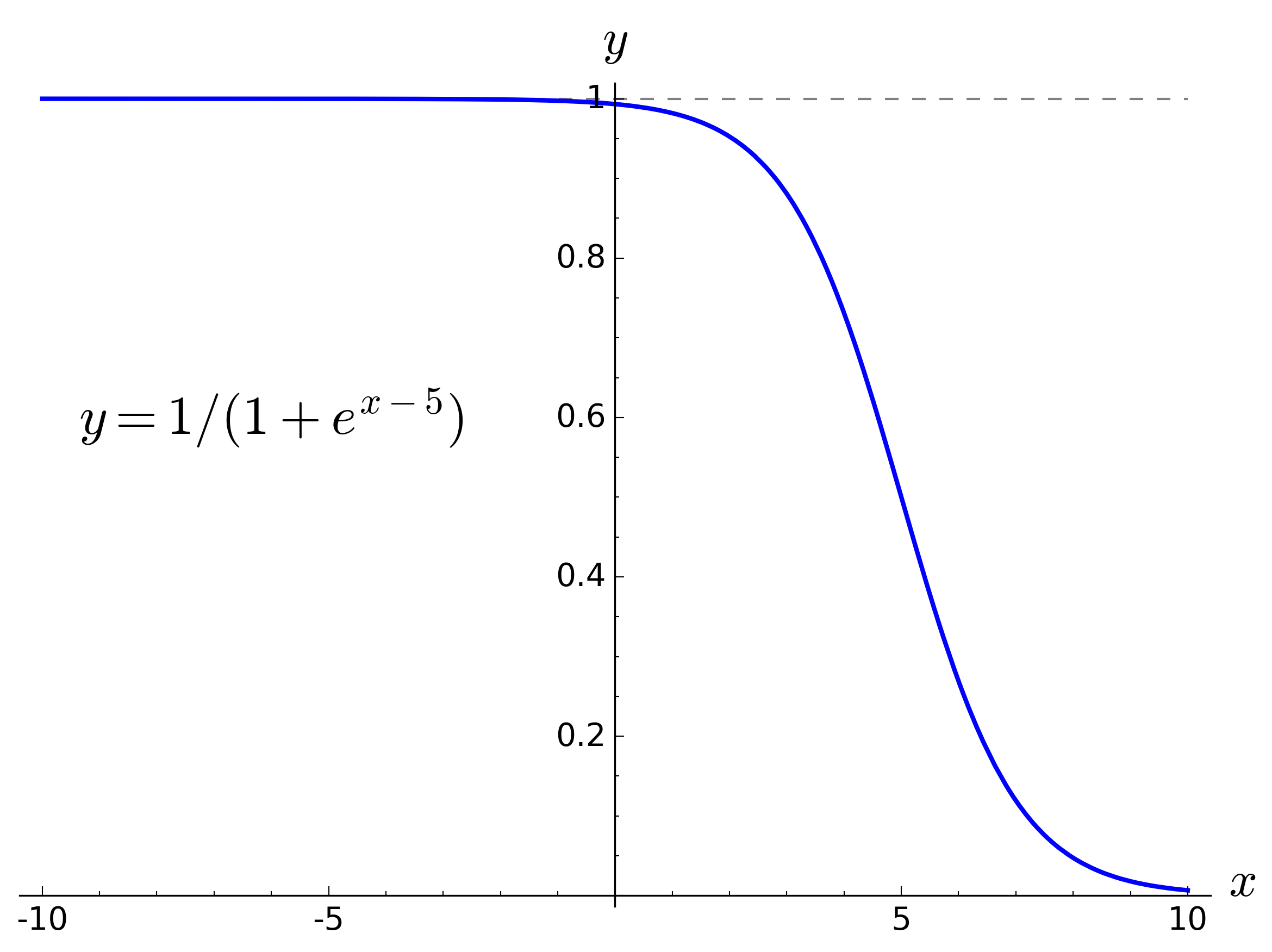
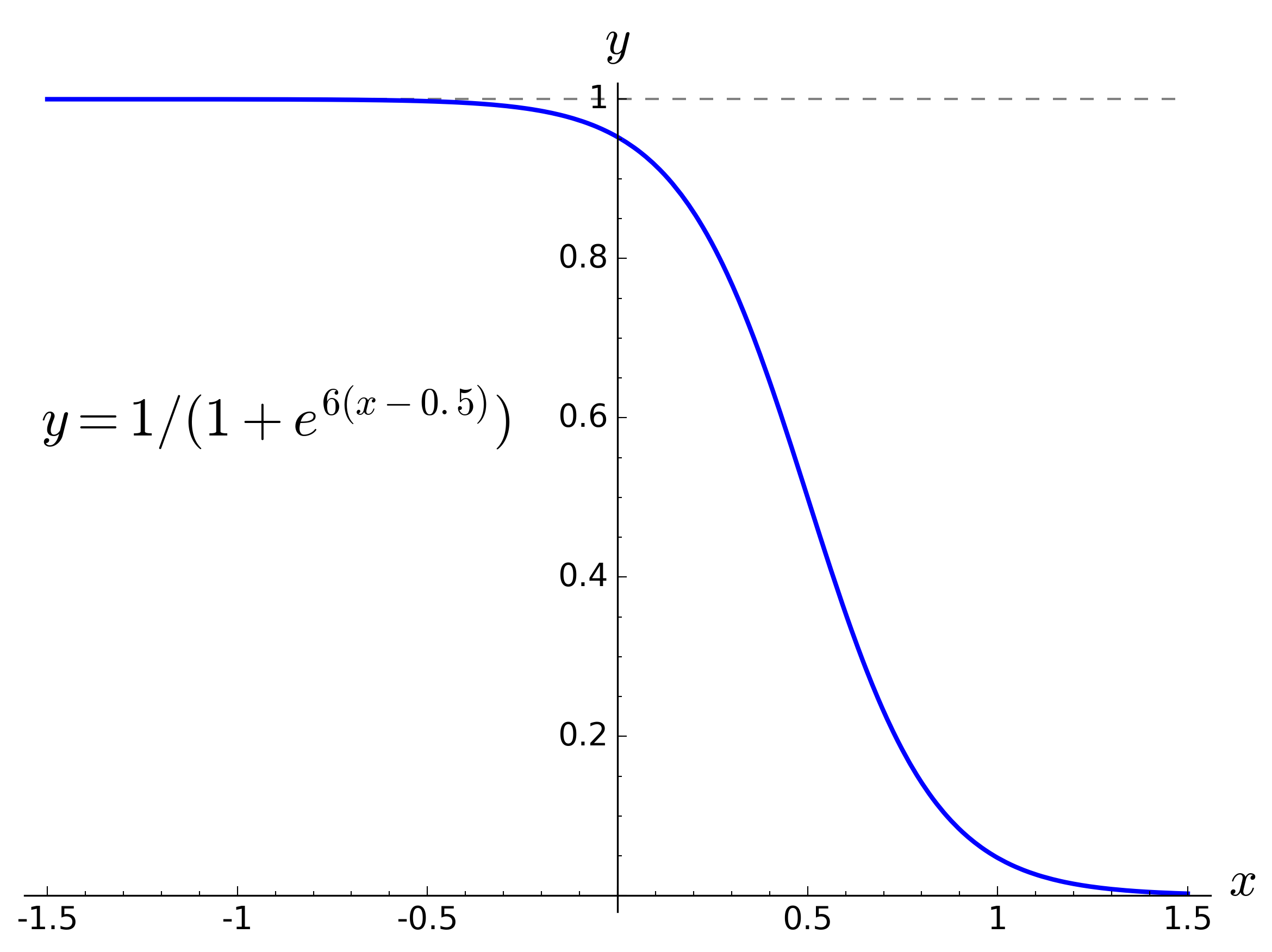
These versions use the natural logarithm base (e), rather than 10, say, but as shown below the actual base value is irrelevant.

For those not interested in the mathematical details, please skip to the Summary Table at the end of the post where all the results are summarised in one combined table.

The general form of the endurance equation is:

ε(ρ) = a√(μ2-wr2) / (1 + bec(ρ-0.5))	…(9)
where:
ε = engine endurance
a, b and c = constants (‘c’ is not the speed of light here)
μ = universal maximum warp speed
wr = rated Warp speed of the ship/engine
ρ = p / pr
p = actual engine power
pr = rated engine full (100%) power

The Lorentzian term √(μ²-w_r²) in the numerator is designed to limit the endurance as the rated Warp speed (w_r) increases. This changes the endurance characteristics for different rated Warp speeds. It makes the endurance approach zero as the rated Warp speed approaches the universal maximum Warp limit (μ).

By setting the exponent to ρ-0.5, the endurance curve is symmetric about ρ=0.5.

The constant a, in conjunction with √(μ²-w_r²), forms the upper limit (asymptote) of the sigmoid function and becomes a scaling factor that depends on the units used to measure endurance.

The constants b and c can be determined by making the following assumptions:

1. Endurance at half power (ρ=0.5) is half the maximum endurance (i.e. ε(0.5) = a√(μ²-w_r²)/2). This also makes the maths below simpler.
2. A Starfleet regulation states that for a Starship to be rated at a particular Warp speed (w_r), its engine must be able to sustain that Warp speed for a minimum period of time (ε_r).

For brevity, we will assign k = √(μ²-w_r²) in the follows calculations. Note k is a constant for each rated Warp speed.

Substituting Assumption 1, ε(0.5)=a√(μ²-w_r²)/2=ak/2, into Equation 9 allows the value of b to be determined as follows:

ε(0.5) = ak/(1 + bec(0.5-0.5)) = ak/(1 + be0) = ak/(1 + b) = ak/2
=> (1 + b) = 2
=> b = 1

Putting this value of b back into Equation 9 gives:

ε(ρ) = ak / (1 + ec(ρ-0.5))

…(10)

Substituting Assumption 2, ε(1) = ε_r, into Equation 10 allows the value of c to be determined as follows:

ε(1) = ak/(1 + ec(1-0.5)) = ak/(1 + ec/2) = εr
=> εr(1 + ec/2) = ak
=> εr + εrec/2 = ak
=> εrec/2 = ak – εr
=> ec/2 = (ak – εr)/εr = ak/εr – 1
=> c/2 = log(ak/εr – 1)
=> c = 2log(ak/εr – 1)

Putting this value of c back into Equation 10 above gives:

ε(ρ)	= ak / (1 + e2log(ak/εr – 1)(ρ – 1/2))
	= ak / (1 + e(2ρ – 1)log(ak/εr – 1))

Which, remembering, e^nlog(x) = xⁿ, simplifies to:

ε(ρ) = ak / (1 + (ak/εr – 1)(2ρ-1))	…(11)
where:
ε = engine endurance
a = constant unit scaling factor
k = √(μ2-wr2)
wr = rated Warp speed of the ship
εr = endurance at full power (ρ=1)
ρ = p / pr
p = actual engine power
pr = rated engine full (100%) power

Finally, let’s provide some concrete values for μ, a and ε_r so we can calculate some actual results. We will stick with μ=10 for the universal Warp limit. Let’s use a (Earth) day as the endurance unit. Setting ε_r to 0.5 days (i.e. 12 hours) as the minimum period the engine must sustain the rated Warp speed.

Noting that k will range between 0 and 10 (mostly nearer 10), setting a to 10 will give a maximum endurance of 100 days. This seems about right. Substituting μ=10, a=10 and ε_r=0.5 into Equation 11 gives:

ε(ρ) = 10√(100-wr2) / (1 + (20√(100-wr2) – 1)(2ρ-1)) days	…(12)
where:
wr = rated Warp speed of the ship
ρ = p / pr

A plot of endurance at different rated Warp speeds is shown below:

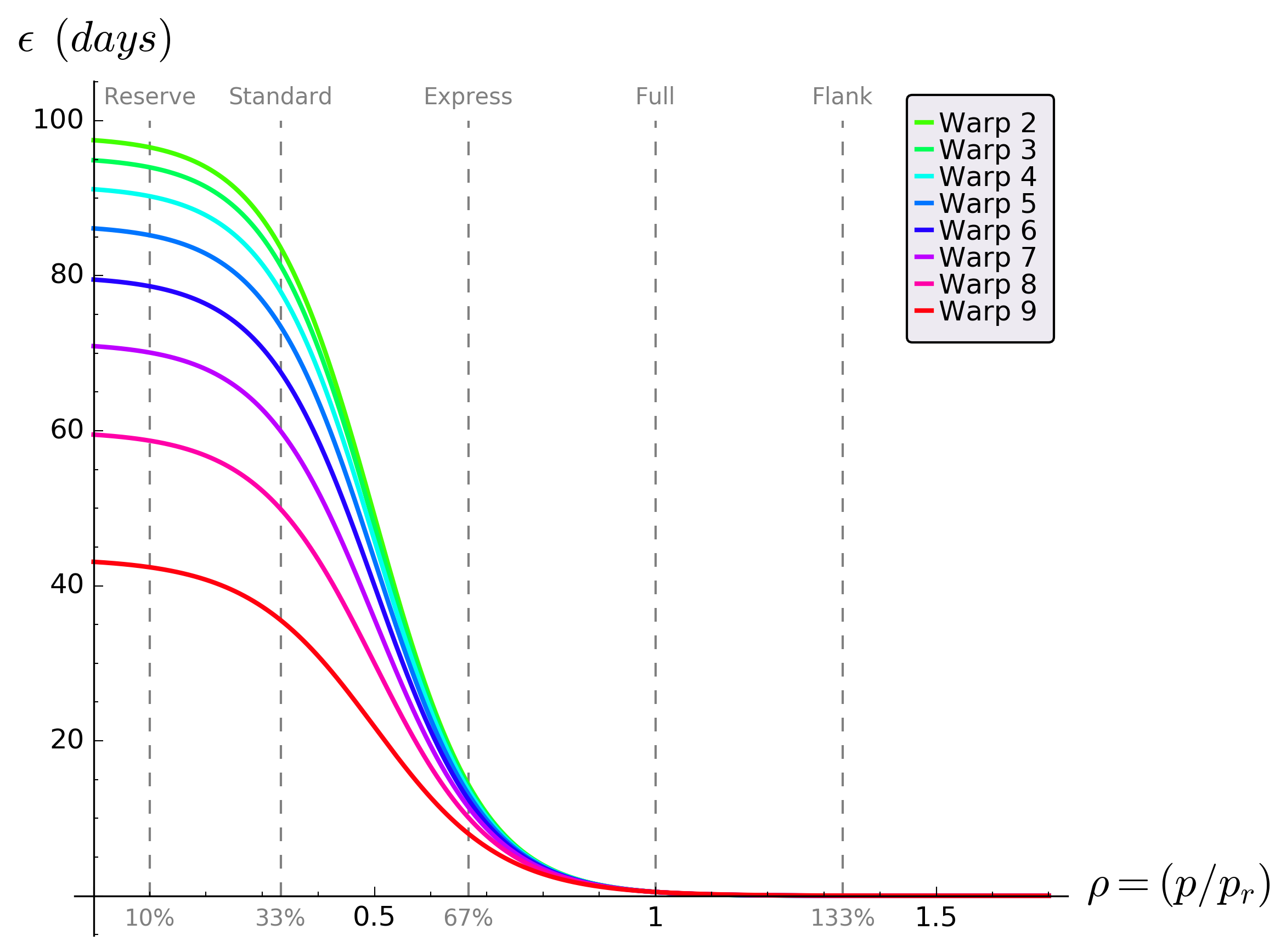
The following points can be drawn from this plot:

• Overall engine endurance declines progressively as the rated Warp speeds increase. Put simply, high performance engines need more frequent maintenance.
• All the individual lines meet at (ρ=1, ε=0.5), although it is hard to see in the plot.
• For any given rated Warp speed, the endurance declines significantly as the power ratio (ρ) increases. In particular, running at standard (33%) power provides much better endurance than express (67%) or higher power ratios.

Table 7 below is a tabular version of the graph above. It shows engine endurance times for the designated power settings for different rated Warp speeds.

Rated	Reserve	Standard	Express	Full	Flank	Maximum
Warp	(10%)	(33%)	(67%)	(100%)	(133%)	(167%)
2	3.2 mth	2.7 mth	2.1 wk	12.0 hr	21.5 min	38.4 sec
3	3.1 mth	2.7 mth	2.0 wk	12.0 hr	21.9 min	39.8 sec
4	3.0 mth	2.6 mth	2.0 wk	12.0 hr	22.5 min	42.0 sec
5	2.8 mth	2.4 mth	1.9 wk	12.0 hr	23.4 min	45.3 sec
6	2.6 mth	2.2 mth	1.8 wk	12.0 hr	24.7 min	50.4 sec
7	2.3 mth	2.0 mth	1.6 wk	12.0 hr	26.6 min	58.8 sec
8	1.9 mth	1.6 mth	1.4 wk	12.0 hr	30.0 min	1.2 min
9	1.4 mth	1.2 mth	1.1 wk	12.0 hr	37.3 min	1.9 min

Table 7 Endurance Times for Different Rated Warp Speeds (μ=10)

Table 7 clearly shows that the endurance at full speed is the same (0.5 day = 12 hr) for each rated Warp speed in accordance with Assumption 2 above.

It also shows, which is not clear from the graph, that the engine endurance of overloaded power settings (i.e. flank and maximum) are dramatically less than full power, measured in only minutes or seconds. This plays into the idea that, in an emergency, it is possible to squeeze a bit more speed from the engine but only for comparatively short periods.

Summary

The various results above can be combined into a single summary table. Table 8 below shows the following information:

• Warp speed (at the designated power setting)
• Endurance (maximum time the engine can run before maintenance)
• Maximum distance before maintenance (Warp speed x endurance time)
• Time to travel 1 lightyear (at the specified Warp speed)
• Energy (fuel) to travel 1 lightyear in an arbitrary unit. In this case we have used kilograms of antimatter

for ships of different rated Warp speeds running at Starfleet designated power settings. The data is based on the equations developed earlier.

Rated Warp	Designation	Reserve	Standard	Express	Full	Flank	Maximum
	Power %	10%	33%	67%	100%	133%	167%
2	Warp	1.3	1.7	1.9	2.0	2.1	2.2
	Endurance	3.2 mth	2.7 mth	2.1 wk	12.0 hr	21.5 min	38.4 sec
	Distance	0.59 ly	1.1 ly	0.30 ly	0.01 ly	0.00 ly	0.00 ly
	Time/ly	5.4 mth	2.5 mth	1.6 mth	1.2 mth	4.3 wk	3.6 wk
	Fuel/ly	0.2 kg	0.3 kg	0.4 kg	0.4 kg	0.4 kg	0.5 kg
3	Warp	2.3	2.6	2.9	3.0	3.1	3.2
	Endurance	3.1 mth	2.7 mth	2.0 wk	12.0 hr	21.9 min	39.8 sec
	Distance	4.6 ly	9.7 ly	2.8 ly	0.14 ly	0.01 ly	0.00 ly
	Time/ly	2.9 wk	1.2 wk	5.0 day	3.7 day	2.9 day	2.5 day
	Fuel/ly	0.5 kg	0.7 kg	0.9 kg	0.9 kg	1.0 kg	1.1 kg
4	Warp	3.2	3.6	3.9	4.0	4.1	4.2
	Endurance	3.0 mth	2.6 mth	2.0 wk	12.0 hr	22.5 min	42.0 sec
	Distance	40 ly	88 ly	27 ly	1.4 ly	0.05 ly	0.00 ly
	Time/ly	2.3 day	21.1 hr	12.1 hr	8.8 hr	6.9 hr	5.8 hr
	Fuel/ly	1.1 kg	1.4 kg	1.6 kg	1.7 kg	1.8 kg	1.9 kg
5	Warp	4.2	4.6	4.9	5.0	5.1	5.2
	Endurance	2.8 mth	2.4 mth	1.9 wk	12.0 hr	23.4 min	45.3 sec
	Distance	351 ly	809 ly	258 ly	14 ly	0.57 ly	0.02 ly
	Time/ly	5.8 hr	2.2 hr	1.2 hr	52.6 min	41.4 min	34.3 min
	Fuel/ly	1.9 kg	2.4 kg	2.7 kg	2.9 kg	3.0 kg	3.1 kg
6	Warp	5.2	5.6	5.9	6.0	6.1	6.2
	Endurance	2.6 mth	2.2 mth	1.8 wk	12.0 hr	24.7 min	50.4 sec
	Distance	3.1 kly	7.3 kly	2.4 kly	137 ly	6.0 ly	0.25 ly
	Time/ly	36.3 min	13.3 min	7.4 min	5.3 min	4.1 min	3.4 min
	Fuel/ly	3.1 kg	3.8 kg	4.2 kg	4.5 kg	4.7 kg	4.8 kg
7	Warp	6.2	6.6	6.9	7.0	7.1	7.2
	Endurance	2.3 mth	2.0 mth	1.6 wk	12.0 hr	26.6 min	58.8 sec
	Distance	27 kly	65 kly	22 kly	1.4 kly	65 ly	2.9 ly
	Time/ly	3.7 min	1.3 min	44.4 sec	31.5 sec	24.7 sec	20.5 sec
	Fuel/ly	4.8 kg	5.8 kg	6.4 kg	6.8 kg	7.1 kg	7.4 kg
8	Warp	7.2	7.6	7.9	8.0	8.1	8.2
	Endurance	1.9 mth	1.6 mth	1.4 wk	12.0 hr	30.0 min	1.2 min
	Distance	233 kly	546 kly	198 kly	14 kly	724 ly	36 ly
	Time/ly	21.7 sec	7.9 sec	4.4 sec	3.2 sec	2.5 sec	2.1 sec
	Fuel/ly	7.3 kg	8.8 kg	9.9 kg	10.6 kg	11.2 kg	11.6 kg
9	Warp	8.2	8.6	8.9	9.0	9.1	9.2
	Endurance	1.4 mth	1.2 mth	1.1 wk	12.0 hr	37.3 min	1.9 min
	Distance	1.8 Mly	4.1 Mly	1.6 Mly	137 kly	8.8 kly	535 ly
	Time/ly	2.0 sec	0.75 sec	0.43 sec	0.32 sec	0.25 sec	0.21 sec
	Fuel/ly	11.7 kg	14.6 kg	16.9 kg	18.5 kg	19.8 kg	20.9 kg
9.5	Warp	8.8	9.2	9.4	9.5	9.6	9.6
	Endurance	4.3 wk	3.5 wk	6.3 day	12.0 hr	46.9 min	3.0 min
	Distance	4.7 Mly	9.9 Mly	4.1 Mly	433 kly	34 kly	2.5 kly
	Time/ly	0.55 sec	0.22 sec	0.13 sec	100 msec	83 msec	72 msec
	Fuel/ly	15.8 kg	20.9 kg	25.3 kg	28.8 kg	31.9 kg	34.8 kg

Table 8 Rated Warp Summary Table

For example, consider a Warp 5 rated ship. At Standard Warp, it will travel at Warp 4.6 which it can sustain for 2.4 months, or just over 800 lightyears, before maintenance is required. At this speed, it will take 2.2 hours and use 2.4 kg of antimatter for each lightyear travelled.

In an emergency, it can travel at Warp 5.2 but only for 45 seconds.

It is also worth noting that Standard Warp provides the best total range for a given rated Warp (i.e. the maximum distance travelled before engine maintenance is required). This agrees with commonsense that there is a “sweet spot” that balances engine endurance and raw speed.

In this post we have:

• Proposed an alternative log base-10 Warp scale that more realistically reflects the vastness of the Universe and makes it more navigable in human time frames
• Developed Warp Power, Energy and Efficiency pseudo-equations by combining relativistic and classical mechanics which provides a robust mathematical underpinning of a universal Warp speed limit
• Introduced the notion of engine endurance to restrict the distance Warp capable ships can travel at various Warp speeds before engine maintenance is required

---

STAR TREK and related marks are trademarks of CBS Studios Inc.